Antena de telefonía fija
Problema 4 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
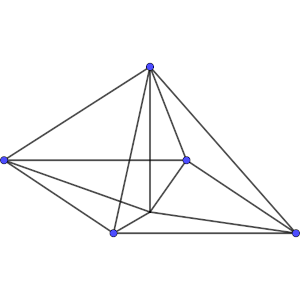
Una antena de telefonía se fija verticalmente sobre una base rectangular horizontal, de vértices ABCD, con cables que van desde el extremo superior de la antena a los cuatro vértices de la base.
Conocemos la longitud de tres cables, que son:
El cable que va del vértice A a la antena, que tiene a metros.
El cable que va del vértice B a la antena, que tiene b metros.
El cable que va del vértice C a la antena, que tiene c metros.
Estos tres datos permiten determinar la longitud del cuarto cable, que se une al vértice D. Calcula, en función de a, b y c, la longitud del cable que falta.
Solución: Aquí.
Solución a un sorteo justo
Problema 3 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
Para elegir un elemento del conjunto A = {01, 02, 03, 04, 05, 06, 07, 08, 09, 10, 11, 12, 13, 14, 15} ejecutamos el siguiente procedimiento:
En primer lugar, ponemos en una bolsa z bolas marcadas con un 0 y u bolas marcadas con un 1, y elegimos una bola, que indicará la primera cifra del elemento que elegiremos finalmente.
En segundo lugar, si ha salido un 0, pondremos en una segunda bolsa nueve bolas numeradas 1, 2, 3, 4, 5, 6, 7, 8, y 9 (una de cada), mientras que si ha salido un 1, sólo pondremos en la segunda bolsa seis bolas numeradas 0, 1, 2, 3, 4, y 5 (una de cada). A continuación extraeremos una bola de esta segunda bolsa, que será la segunda cifra de el elemento que escogeremos.
Calcula cuáles han de ser los valores mínimos que pueden tener z y u para que los 15 elementos de A tengan todos la misma probabilidad de ser escogidos.

Solución:
(more…)
Un sorteo justo
Problema 3 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
Para elegir un elemento del conjunto A = {01, 02, 03, 04, 05, 06, 07, 08, 09, 10, 11, 12, 13, 14, 15} ejecutamos el siguiente procedimiento:
En primer lugar, ponemos en una bolsa z bolas marcadas con un 0 y u bolas marcadas con un 1, y elegimos una bola, que indicará la primera cifra del elemento que elegiremos finalmente.
En segundo lugar, si ha salido un 0, pondremos en una segunda bolsa nueve bolas numeradas 1, 2, 3, 4, 5, 6, 7, 8, y 9 (una de cada), mientras que si ha salido un 1, sólo pondremos en la segunda bolsa seis bolas numeradas 0, 1, 2, 3, 4, y 5 (una de cada). A continuación extraeremos una bola de esta segunda bolsa, que será la segunda cifra de el elemento que escogeremos.
Calcula cuáles han de ser los valores mínimos que pueden tener z y u para que los 15 elementos de A tengan todos la misma probabilidad de ser escogidos.

Solución: Aquí.
Solución a el área de un triángulo
Problema 2 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
Conocemos los dos lados de un triángulo, que son a y b.
¿Cuál es el máximo valor que puede tener el área del triángulo?

Solución:
(more…)
El área de un triángulo
Problema 2 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
Conocemos los dos lados de un triángulo, que son a y b.
¿Cuál es el máximo valor que puede tener el área del triángulo?

Solución: Aquí.
Solución a tableros
Problema 1 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
Tenemos un tablero cuadrado 5×5 y las 5 piezas en forma de “L” (excepto una que es un cuadrado) que se muestran:
Hay muchas maneras de situar las piezas de forma que llenen el tablero, se muestran tres ejemplos.
a) Determina de cuántas formas diferentes se pueden situar las cinco piezas para llenar el tablero, que siempre consideramos con la misma orientación (la pieza cuadrada no se distingue si está girada o no, así que siempre se considera que está puesta de la misma forma salvo que cambiemos su ubicación).
b) ¿En cuántas de las ocasiones la pieza cuadrada queda situada exactamente en el centro?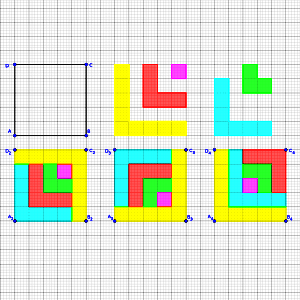
Solución:
(more…)
Tableros
Problema 1 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
Tenemos un tablero cuadrado 5×5 y las 5 piezas en forma de “L” (excepto una que es un cuadrado) que se muestran:
Hay muchas maneras de situar las piezas de forma que llenen el tablero, se muestran tres ejemplos.
a) Determina de cuántas formas diferentes se pueden situar las cinco piezas para llenar el tablero, que siempre consideramos con la misma orientación (la pieza cuadrada no se distingue si está girada o no, así que siempre se considera que está puesta de la misma forma salvo que cambiemos su ubicación).
b) ¿En cuántas de las ocasiones la pieza cuadrada queda situada exactamente en el centro?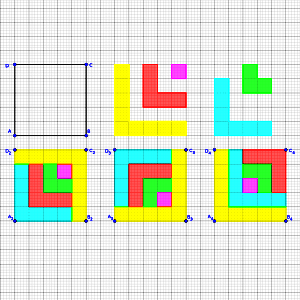
Solución: Aquí.
Solución a ¿cuántos enteros?
Problema 0 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
Calcula cuántos números enteros son solución de la siguiente inecuación:
|2021 – |x|| ≤ 2022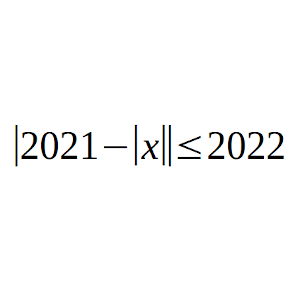
Solución:
(more…)
¿Cuántos enteros?
Problema 0 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
Calcula cuántos números enteros son solución de la siguiente inecuación:
|2021 – |x|| ≤ 2022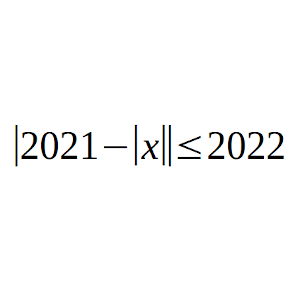
Solución: Aquí.
Solución a tres cubos
Problema 5 del nivel B fase comarcal de Alicante de la Olimpiada de la Comunidad Valenciana 2021 Se dirige a una edad de: 14 - 15 años
Demuestra que la suma tres cubos consecutivos es múltiplo de 9.

Solución:
(more…)