Problema 3 de la Fase Local de la Olimpiada Española de Matemáticas 2022 (viernes tarde)
Se dirige a una edad de: 16-17 años
Hallar todas las ternas de números reales (a, b, c) que cumplan el sistema:
a + b + c = 3
2^a + 2^b + 2^c = 7
2^-a + 2^-b = ¾

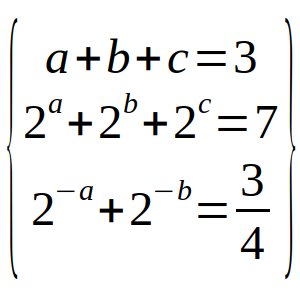
Solución:

Lo primero que debemos observar es que hay una función no polinómica implicada, la potencia de base 2. Sin embargo, hay ecuaciones que no lo tienen. Un primer avance supone escribir la ecuación a + b + c = 3 de forma que contenga potencias de 2 de exponentes a, b y c.

Aprovechamos que 2^{a + b + c} = 2^a·2^b·2^c = 2³ = 8 para escribir la primera ecuación con potencias de base 2. Y, evidentemente, la última es muy fácil expresarla en forma de potencias de base 2 y exponentes de a y b.

2^a·2^b·2^c = 8
2^a + 2^b + 2^c = 7
1/2^a + 1/2^b = ¾

En un segundo paso, cambiamos la función 2^a por una nueva variable x, 2^b por y y 2^c por z.

xyz = 8
x + y + z = 7
1/x + 1/y = ¾

Ahora es un sistema más similar a los que habitualmente nos enfrentamos, con polinomios de grado 3, 1 y 2 (si eliminásemos denominadores).

xyz = 8
x + y + z = 7
(x + y)/(xy) = ¾

Sin embargo, podemos aprovechar la simetría de las dos primeras ecuaciones, ya que xy = 8/z y x + y = 7 – z, por lo que podemos escribir la última ecuación con ayuda de la única variable z:

(7 – z)/(8/z) = ¾

Simplificar las fracciones que componen la fracción, multiplicando numerador y denominador por z, deja la expresión:

z(7 – z)/8 = ¾

Y multiplicando ambos extremos de la igualdad por 8, nos deja una ecuación de segundo grado:

z(7 – z) = 6

Que es equivalente a

0 = z² – 7z + 6

Evidentemente, aplicando la conocida fórmula para ecuaciones de segundo grado, nos deja dos soluciones, 6 y 1, que podemos estudiar por separado:

Si z = 6, tenemos que las variables x e y deben cumplir

xy = 4/3
x + y = 1

Despejando y = 1 – x, y sustituyendo, nos lleva a la ecuación 3x² – 3x + 4 = 0, que no tiene soluciones reales (ya que su discriminante, la expresión que habitualmente encontramos dentro de la raíz cuadrada, es negativo), por lo que no da lugar a ninguna solución para el sistema.

Sin embargo, si z = 1 tenemos:

xy = 8
x + y = 6

De nuevo, despejando y = 6 – x y sustituyendo en la primera ecuación, nos lleva a x² – 6x + 8 = 0, que da lugar a dos soluciones, x = 2 (y por tanto, y = 4), y x = 4, con lo que y = 2.

Por lo tanto, sólo tendríamos dos soluciones (dos ternas, por tanto):

x = 2, y = 4, z = 1, con lo que tenemos la terna (1, 2, 0), y x = 4, y = 2, z = 1, que da lugar a la terna (2, 1, 0).