Problema 4 del nivel A de la Fase Comarcal de la Olimpiada de la Comunidad Valenciana Se dirige a una edad de: 12-13 años
Calcula cuánto mide el perímetro del hexágono sabiendo que las áreas de las dos zonas rayadas son, respectivamente, 10,3923 cm² y 1,4494 cm².
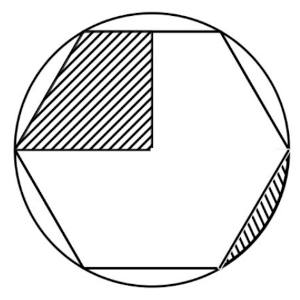
Solución:
La solución más obvia, que inicialmente no vi, era completar el círculo, ya que lo que hay en el interior del hexágono es un cuarto de hexágono, y la parte de fuera del hexágono es un sexto de lo que le falta al hexágono para rellenar la circunferencia.
Por tanto, el área de la circunferencia sería 4·10,3923 + 6·1,4494 = 50,2656.
Puesto que el área de un círculo es π·r², podemos obtener el radio al cuadrado si dividimos este valor por π, que da 16.
Es decir, que el radio al cuadrado da 16 cm², por lo que vale 4 cm este radio.
Pero el radio en el que está inscrito el hexágono mide lo mismo que su lado, porque se puede dividir en seis triángulos equiláteros, como podemos ver en la figura.
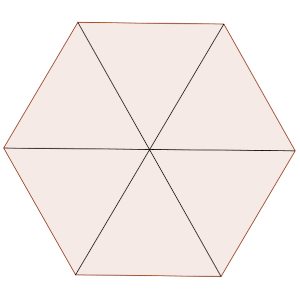
Por lo tanto, su perímetro vale 6·4 = 24 cm.
Inicialmente, yo hice algo mucho más complicado, ya que me di cuenta de que la zona interior era un triángulo equilátero y medio, y pensé que sólo con ese dato podría conseguirlo. Calculé el área de un triángulo equilátero de lado 2, descomponiéndolo en dos triángulos rectángulos, y me di cuenta de que el dato que me daban era 4 veces mayor, por lo que el triángulo equilátero debía tener lado 4. A partir de ahí, el razonamiento era el mismo.