Problema 2 del viernes de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
Demuestra que para todo n ≥ 2 podemos encontrar n números reales x1, x2, …, xn ≠ 1 de manera que los productos x1·x2·…·xn y (1/(1 – x1))·(1/(1 – x2))·…·(1/(1 – xn)) son iguales.
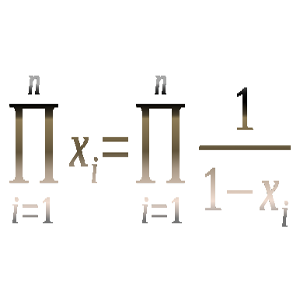
Solución: Aquí.