Problema 4 de la Fase Local de la Olimpiada Española de Matemáticas 2023 (viernes mañana)
Se dirige a una edad de: 16-17 años

Consideramos un paralelogramo ABCD.

Una circunferencia Γ que pasa por el punto A corta a los lados AB y AD en los puntos E y F, respectivamente, y a la diagonal AC en el punto G.

La prolongación de la recta FG corta al lado BC en H, y la prolongación de EG corta al lado CD en I.

Demuestra que la recta HI es paralela a EF.

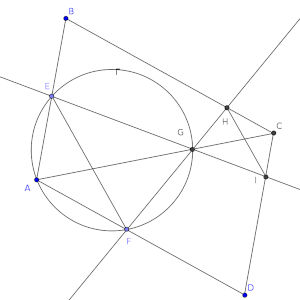
Solución:

Los argumentos que se pueden dar en este problema son muy numerosos. Puesto que está implicada una circunferencia y un paralelogramo, muchos ángulos están repetidos.

Usando el ángulo central, es muy sencillo ver que un paralelogramo está inscrito en una circunferencia (es decir, es cíclico) si y sólo si dos de sus ángulos opuestos suman 180º.

Esto nos permite ver que el cuadrilátero AEGF es inscrito, y por tanto el GHCI también lo es, ya que comparten ángulo en G por formarlo las mismas rectas, y también en C, por ser ABCD paralelogramo.

Lo único que tenemos que ver es que el ángulo que forma el segmento HI con CB (o con CD) es el mismo que el que forma EF con AD (o con AB).

Pero claro, precisamente por esa razón, el ángulo que se forma en AFE es el mismo que AGF, que es el mismo que CGH y por tanto es el mismo que CIH. Que es justo lo que necesitamos.