Problema 1 del nivel B fase autonómica de la Olimpiada de la Comunidad Valenciana 2018
Se dirige a una edad de: 13-14 años

Tenemos dos naranjas de 5 centímetros de radio.

¿Cuál es la altura mínima que debe tener un bol semiesférico para que podamos poner dentro las dos naranjas sin que sobresalgan?

Si tenemos un bol del tamaño indicado en el apartado anterior, ¿a qué altura respecto al fondo del bol quedan los puntos en los que las naranjas tocan el bol?

Solución:

Para este tipo de problemas, en los que aparecen varias tangencias y círculos, debemos trazar los radios de las circunferencias que sean importantes en el contexto del dibujo.

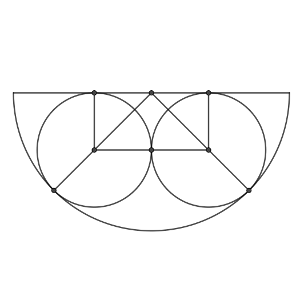
Dada la simetría, tendremos que desde el centro del borde del bol, la perpendicular separa a las dos naranjas, por lo que el radio que pasa por el centro de las naranjas toca en el punto de tangencia.

Por lo tanto, desde el centro hasta el punto donde la naranja toca al bol, hay cinco centímetros, y el resto del segmento que forma el radio del bol es la hipotenusa de un triángulo rectángulo cuyos catetos miden ambos 5, por lo que, aplicando el Teorema de Pitágoras, ese segmento mide 5·raíz(2), aproximadamente 7,071.

El radio del bol, por tanto, que coincide con la altura del mismo, medirá 5 + 5raíz(2), es decir, aproximadamente 12,071.

En cuanto al punto donde las naranjas tocan al bol, podemos encontrar un triángulo rectángulo en el que esté metido, para calcular su altura.
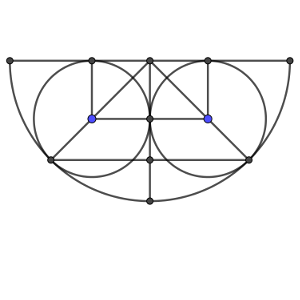Por ejemplo, uniendo los dos puntos donde ambas naranjas tocan el bol, tendremos un triángulo isósceles, semejante al triángulo que se forma desde el centro del semicírculo que forma el bol y los dos centros de las naranjas.

De este triangulo isósceles, tenemos una medida, su lado repetido, que medirá 5 + 5raíz(2), es decir, 12,071. Y del triángulo semejante, tenemos también la medida equivalente (que mediría 5raíz(2), y la altura, que mediría 5.

Por lo tanto, podemos calcular el factor de escala, que sería (5 + 5raíz(2))/5raíz(2), y multiplicarlo por la altura (5), para obtener la altura del triángulo que nos interesa. Manipular esta expresión es algo complicado, los alumnos más avanzados sabrán que 5(5 + 5raíz(2))/5raíz(2) = (5 + 5raíz(2))/raíz(2) = raíz(2)(5 + 5raíz(2))/2 = (5raíz(2) + 10)/2 = 5raíz(2)/2 + 5. Pero aunque no sea así, seguro que podemos calcular su valor aproximado con la calculadora, 8,536.

Y por lo tanto la altura desde el fondo del bol sería 5 + 5raíz(2) – ( 5raíz(2)/2 + 5) = 5raíz(2) – 5raíz(2)/2 = 5raíz(2)/2, o en su versión aproximada, 3,536.