Solución a “Multiplicando”
Problema 1 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
Julián y Juia tienen el encargo de multiplicar dos números primos diferentes, cada uno de dos cifras, uno es el 31 y el otro lo indicamos como ab.
Julia ha multiplicado correctamente 31·ab pero en Julián se ha equivocado y el segundo número lo ha escrito con las cifras cambiadas de orden, es decir, que ha multiplicado 31·ba y en principio no se ha dado cuenta del despiste porque casualmente también multiplicaba dos números primos.
El resultado de Julia es 558 unidades más grande que el de Julián.
¿Cuál es el número que ha usado correctamente Juliana?

Solución:
(more…)
Multiplicando
Problema 1 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
Julián y Juia tienen el encargo de multiplicar dos números primos diferentes, cada uno de dos cifras, uno es el 31 y el otro lo indicamos como ab.
Julia ha multiplicado correctamente 31·ab pero en Julián se ha equivocado y el segundo número lo ha escrito con las cifras cambiadas de orden, es decir, que ha multiplicado 31·ba y en principio no se ha dado cuenta del despiste porque casualmente también multiplicaba dos números primos.
El resultado de Julia es 558 unidades más grande que el de Julián.
¿Cuál es el número que ha usado correctamente Juliana?

Solución: Aquí.
Solución a “Sumar 2024”
Problema 0 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
Tres números de tres cifras suman 2024.
Las nueve cifras que tienen son diferentes.
¿Qué cifra no hemos usado para construir esos tres números?

Solución:
(more…)
Sumar 2024
Problema 0 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
Tres números de tres cifras suman 2024.
Las nueve cifras que tienen son diferentes.
¿Qué cifra no hemos usado para construir esos tres números?

Solución: Aquí.
Solución a “Las tres compañeras”
Problema 4 del nivel C de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023 Se dirige a una edad de: 10 -11 años
Clara, Ana y Elisa van de excursión en autobús y están sentadas en tres asientos, una detrás de otra.
Las tres van vestidas de rojo, blanco y azul (no necesariamente en ese orden) y tienen como aficiones bailar, jugar al baloncesto y jugar al voleibol (aunque tampoco necesariamente en ese orden).
A partir de las pistas siguientes, indica en qué posición está sentada cada una, de qué color van vestidas y su afición.
Pistas:
1.- Clara está sentada entre dos compañeras y le ha prestado la ropa a la que va vestida de rojo.
2.- A Elisa nunca le han gustado los deportes que se practican con balón.
3.- Delante de la que baila, está sentada la que juega a voleibol.
4.- La última de la fila de asientos es la que viste de azul.

Solución:
(more…)
Las tres compañeras
Problema 4 del nivel C de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023 Se dirige a una edad de: 10 -11 años
Clara, Ana y Elisa van de excursión en autobús y están sentadas en tres asientos, una detrás de otra.
Las tres van vestidas de rojo, blanco y azul (no necesariamente en ese orden) y tienen como aficiones bailar, jugar al baloncesto y jugar al voleibol (aunque tampoco necesariamente en ese orden).
A partir de las pistas siguientes, indica en qué posición está sentada cada una, de qué color van vestidas y su afición.
Pistas:
1.- Clara está sentada entre dos compañeras y le ha prestado la ropa a la que va vestida de rojo.
2.- A Elisa nunca le han gustado los deportes que se practican con balón.
3.- Delante de la que baila, está sentada la que juega a voleibol.
4.- La última de la fila de asientos es la que viste de azul.

Solución: Aquí.
Solución a “Una ecuación complicada”
Problema 7 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sea a > 1 un número real.
Encontrar todas las soluciones de la ecuación: raíz(a – raíz(a + x)) = x en función de a.
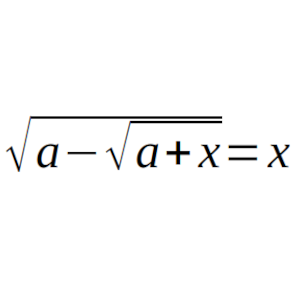
Solución:
(more…)
Una ecuación complicada
Problema 7 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sea a > 1 un número real.
Encontrar todas las soluciones de la ecuación: raíz(a – raíz(a + x)) = x en función de a.
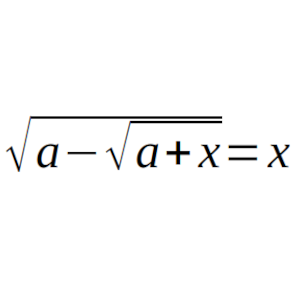
Solución: Aquí.
Solución a “Demasiados cuadrados”
Problema 6 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sean a, b, c tres números enteros, y sea p >= 5 un número primo.
Demostrar que, si an² + bn + c es el cuadrado de un número entero para 2p – 1 valores consecutivos de n, entonces b² – 4ac es un múltiplo de p.

Solución:
(more…)
Demasiados cuadrados
Problema 6 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Sean a, b, c tres números enteros, y sea p >= 5 un número primo.
Demostrar que, si an² + bn + c es el cuadrado de un número entero para 2p – 1 valores consecutivos de n, entonces b² – 4ac es un múltiplo de p.

Solución: Aquí.