Problema 3 del segundo nivel de la Olimpiada de Mayo (2018) Se dirige a una edad de: 12 años
Los 2018 residentes de un pueblo están estrictamente divididos en dos clases: caballeros, que siempre dicen la verdad, y mentirosos, que siempre mienten.
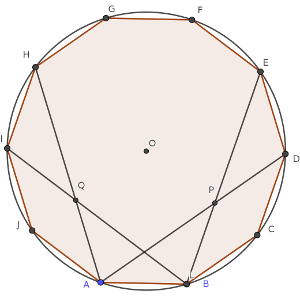
Cierto día todos los residentes se acomodaron alrededor de una circunferencia y cada uno de ellos anunció en voz alta “Mis dos vecinos, el de la izquierda y el de la derecha, son mentirosos”.
A continuación uno de los residentes abandonó el pueblo.
Los 2017 que quedaron se acomodaron nuevamente en una circunferencia (no necesariamente en el mismo orden que antes) y cada uno de ellos anunció en voz alta “Ninguno de mis vecinos, el de la izquierda y el de la derecha, es de mi misma clase”.
Determinar, si es posible, de qué clase es el residente que abandonó el pueblo, caballero o mentiroso.

Solución:
Continue reading Solución a caballeros y mentirosos