Problema 6 de la Olitele (Olimpiada Telemática de Cataluña) 2017 Se dirige a una edad de: 16-17 años
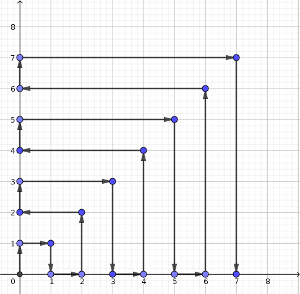
Un robot circula por un plano coordenado de la forma que marca el dibujo.
Así, tras llegar al punto (7, 0), avanzará una unidad en horizontal hasta el (8, 0), subirá en vertical 8 unidades hasta el (8, 8) y retrocederá en horizontal ocho unidades hasta el (0, 8), y así sucesivamente.
Si cada unidad del plano mide un centímetro, ¿en qué coordenadas se encontrará cuando haya recorrido exactamente 2017 centímetros?
Solución: Aquí
Yo diría que se encuentra en el punto (7,44), aunque no es uno de los puntos del robot…
Si no me he confundido, (7, 44) y hacia la izquierda.
Desarrollando:
Cuando acaba de completar un cuadrado de lado n, en el eje Ox si n es impar y en el Oy si n es par, ha recorrido 2*(1/2)n(n+1) + n = n^2 + 2n cm.
Se trata de encontrar el mayor n tal que n^2 + 2n < 2017 n^2 + 2n + 1 = (n+1)^2 < 2018 . Como 45^2 = 2025 y 44^2 = 1936, nuestro n es 43.
Como 43^2 + 2*43 = 44^2 – 1 = 1935, despues de completar un cuadrado de lado 43, situado en el eje Ox, le quedan por recorrer 2017 – 1935 = 82 cm. Serán uno a la derecha, y llega a (44, 0), 44 hacia arriba, llegando a (44, 44) y los 37 restantes hacia la izquierda, quedando en el (7, 44).