Home » 2018 (Page 2)
Yearly Archives: 2018
Solución a hermanos a pares
Problema 5 del nivel B fase comarcal de la Olimpiada de la Comunidad Valenciana 2018 Se dirige a una edad de: 13-15 años
Un grupo de jóvenes está formado por 5 pares de hermanos. Cada uno de los 10 jóvenes tiene una edad diferente comprendida entre 4 y 13 años (incluidas ambas edades).
Las sumas de las edades de las parejas de hermanos son 10, 13, 17, 22 y 23. Si Juan tiene 9 años, ¿qué edad tiene su hermano?

Solución:
(more…)
Hermanos a pares
Problema 5 del nivel B fase comarcal de la Olimpiada de la Comunidad Valenciana 2018 Se dirige a una edad de: 13-15 años
Un grupo de jóvenes está formado por 5 pares de hermanos. Cada uno de los 10 jóvenes tiene una edad diferente comprendida entre 4 y 13 años (incluidas ambas edades).
Las sumas de las edades de las parejas de hermanos son 10, 13, 17, 22 y 23. Si Juan tiene 9 años, ¿qué edad tiene su hermano?

Solución: Aquí.
Solución a cruzando el río
Problema 1 de la prueba de selección de Estalmat 2018 Se dirige a una edad de: 11-12 años
En una de las orillas de un río hay 3 adultos, 2 niños y una barca de remos muy pequeña.
Queremos que todas las personas crucen el río utilizando la barca.
En la barca sólo caben o bien un solo adulto o bien 2 niños.
Todos saben remar y está permitido que un niño vaya solo en la barca.
Entendemos por viaje a remar de un lado al otro del río:
a) ¿Cuál es el mínimo número de viajes que habrá que hacer para que todas las personas crucen el río? Explica cómo has llegado al resultado.
b) ¿Y si hubiera 8 adultos y 2 niños? ¿Y si hubiera 100 adultos y 2 niños? Explica cómo has llegado a tus respuestas.
c) Explica cómo podemos encontrar el mínimo número de viajes necesarios para cualquier número de adultos y 2 niños.
d) Si ahora, en una de las orillas hay 4 adultos y 3 niños ¿cuál es el número mínimo de viajes que habrá que hacer para que todas las personas crucen el río? ¿Cómo los harías?
e) ¿Y si hubiera 8 adultos y 3 niños? ¿Y si hubiera 100 adultos y 3 niños? Explica cómo podemos encontrar el mínimo número de viajes necesarios para cualquier número de adultos y 3 niños.
f) Explica cómo podemos encontrar el mínimo número de viajes necesarios para cualquier número de adultos y cualquier número de niños.
Solución:
(more…)
Cruzando el río
Problema 1 de la prueba de selección de Estalmat 2018 Se dirige a una edad de: 11-12 años
En una de las orillas de un río hay 3 adultos, 2 niños y una barca de remos muy pequeña.
Queremos que todas las personas crucen el río utilizando la barca.
En la barca sólo caben o bien un solo adulto o bien 2 niños.
Todos saben remar y está permitido que un niño vaya solo en la barca.
Entendemos por viaje a remar de un lado al otro del río:
a) ¿Cuál es el mínimo número de viajes que habrá que hacer para que todas las personas crucen el río? Explica cómo has llegado al resultado.
b) ¿Y si hubiera 8 adultos y 2 niños? ¿Y si hubiera 100 adultos y 2 niños? Explica cómo has llegado a tus respuestas.
c) Explica cómo podemos encontrar el mínimo número de viajes necesarios para cualquier número de adultos y 2 niños.
d) Si ahora, en una de las orillas hay 4 adultos y 3 niños ¿cuál es el número mínimo de viajes que habrá que hacer para que todas las personas crucen el río? ¿Cómo los harías?
e) ¿Y si hubiera 8 adultos y 3 niños? ¿Y si hubiera 100 adultos y 3 niños? Explica cómo podemos encontrar el mínimo número de viajes necesarios para cualquier número de adultos y 3 niños.
f) Explica cómo podemos encontrar el mínimo número de viajes necesarios para cualquier número de adultos y cualquier número de niños.
Solución: Aquí.
Solución a distancias en un paralelogramo
Problema 4 del segundo nivel de la Olimpiada de Mayo (2018) Se dirige a una edad de: 14 años
En un paralelogramo ABCD, sea M el punto del lado BC tal que MC = 2BM y sea N el punto del lado CD tal que NC = 2DN.
Si la distancia del punto B a la recta AM es 3, calcular la distancia del punto N a la recta AM.
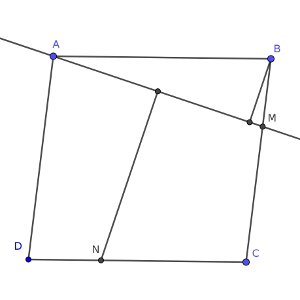
Solución:
(more…)
Distancias en un paralelogramo
Problema 4 del segundo nivel de la Olimpiada de Mayo (2018) Se dirige a una edad de: 14 años
En un paralelogramo ABCD, sea M el punto del lado BC tal que MC = 2BM y sea N el punto del lado CD tal que NC = 2DN.
Si la distancia del punto B a la recta AM es 3, calcular la distancia del punto N a la recta AM.

Solución: Aquí.
Solución a siete números enteros
Problema 4 del primer nivel de la Olimpiada de Mayo (2018) Se dirige a una edad de: 12 años
Ana debe escribir 7 enteros positivos, no necesariamente distintos, alrededor de una circunferencia de manera que se cumplan las siguientes condiciones:
La suma de los siete números es igual a 36.
Si dos números son vecinos la diferencia entre el mayor y el menor es igual a 2 o 3.
Hallar el máximo valor del mayor de los números que puede escribir Ana.
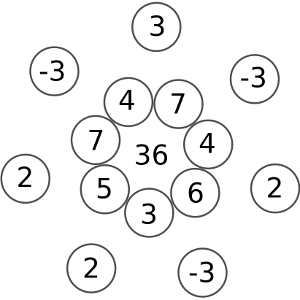
Solución:
(more…)
Siete números enteros
Problema 4 del primer nivel de la Olimpiada de Mayo (2018) Se dirige a una edad de: 12 años
Ana debe escribir 7 enteros positivos, no necesariamente distintos, alrededor de una circunferencia de manera que se cumplan las siguientes condiciones:
La suma de los siete números es igual a 36.
Si dos números son vecinos la diferencia entre el mayor y el menor es igual a 2 o 3.
Hallar el máximo valor del mayor de los números que puede escribir Ana.

Solución: Aquí.
Solución a productos de un conjunto
Problema 2 de la Olimpiada Matemática Femenina Europea (EGMO 2018) Se dirige a una edad de: 17 años
Considere el conjunto A = {1 + 1/k / k = 1, 2, 3,…}.
a) Demuestre que todo entero x ≥ 2 puede ser escrito como producto de uno o más elementos de A, no necesariamente distintos.
b) Para todo entero x ≥ 2, sea f(x) el menor entero tal que x puede ser escrito como f(x) elementos de A, no necesariamente distintos.
Demuestre que existen infinitos pares (x, y) de enteros, con x ≥ 2, y ≥ 2, tales que f(xy) < f(x) + f(y).
Nota: los pares (x, y), (z, t) son diferentes si x es diferente de z o y es diferente de t.
 Solución:
Solución:
(more…)
Productos de un conjunto
Problema 2 de la Olimpiada Matemática Femenina Europea (EGMO 2018) Se dirige a una edad de: 17 años
Considere el conjunto A = {1 + 1/k / k = 1, 2, 3,…}.
a) Demuestre que todo entero x ≥ 2 puede ser escrito como producto de uno o más elementos de A, no necesariamente distintos.
b) Para todo entero x ≥ 2, sea f(x) el menor entero tal que x puede ser escrito como f(x) elementos de A, no necesariamente distintos.
Demuestre que existen infinitos pares (x, y) de enteros, con x ≥ 2, y ≥ 2, tales que f(xy) < f(x) + f(y).
Nota: los pares (x, y), (z, t) son diferentes si x es diferente de z o y es diferente de t.

Solución: Aquí.