Home » Olimpiada Matemática Española (Page 13)
Category Archives: Olimpiada Matemática Española
Un triángulo con 120 grados
Problema 3 del sábado de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
Consideramos un triángulo ABC y un punto D en el lado AC.
Si la longitud de AB y de DC es 1, el ángulo DBC es de 30º, y ABD es de 90º, calcula la longitud de AD.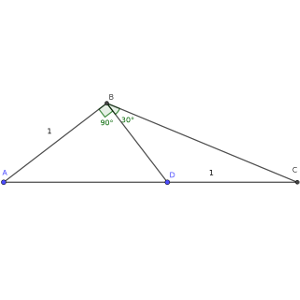
Solución: Aquí.
Solución a desigualdad con números positivos
Problema 2 del sábado de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
Prueba que para todo a, b, c > 0 se cumple la siguiente desigualdad: a²/(b³c) – a/b² ≥ c/b – c²/a.
¿En qué caso se cumple la igualdad?
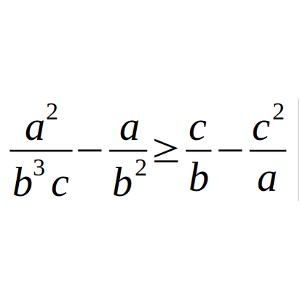 Solución:
Solución:
(more…)
Desigualdad con números positivos
Problema 2 del sábado de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
Prueba que para todo a, b, c > 0 se cumple la siguiente desigualdad: a²/(b³c) – a/b² ≥ c/b – c²/a.
¿En qué caso se cumple la igualdad?
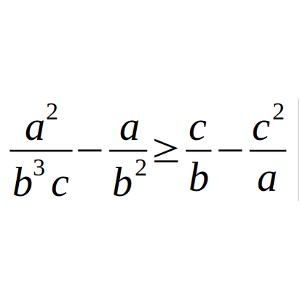
Solución: Aquí.
Solución a comparando conjuntos
Problema 1 del sábado de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
Considera el conjunto de números enteros positivos n cumpliendo 1 ≤ n ≤ 1000000.
En este conjunto, indica si es mayor la cantidad de números que pueden expresarse de la forma a³ + mb², con a, b números naturales y m pertenece al conjunto {0, 2, 4, 6, 8} o la cantidad de números que no pueden expresarse de esa manera.
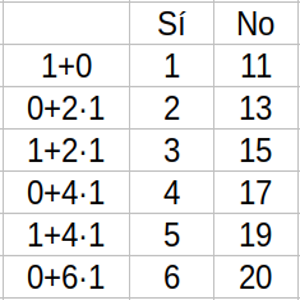
Solución:
(more…)
Comparando conjuntos
Problema 1 del sábado de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
Considera el conjunto de números enteros positivos n cumpliendo 1 ≤ n ≤ 1000000.
En este conjunto, indica si es mayor la cantidad de números que pueden expresarse de la forma a³ + mb², con a, b números naturales y m pertenece al conjunto {0, 2, 4, 6, 8} o la cantidad de números que no pueden expresarse de esa manera.

Solución: Aquí.
Solución a ecuación con polinomios
Problema 6 del viernes de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
Fijamos un número natural k mayor o igual que 1. Encuentra todos los polinomios P(x) que cumplan P(xk) – P(kx) = xkP(x).
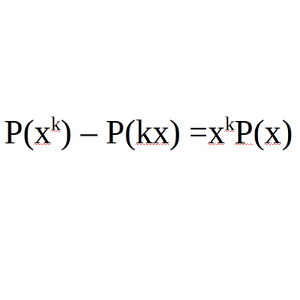
Solución: (more…)
Ecuación con polinomios
Problema 6 del viernes de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
Fijamos un número natural k mayor o igual que 1. Encuentra todos los polinomios P(x) que cumplan P(xk) – P(kx) = xkP(x).
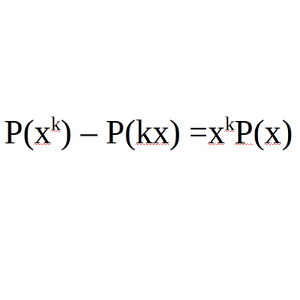
Solución: Aquí.
Solución a expresión compuesta
Problema 5 del viernes de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
¿Existen n y m naturales diferentes de cero de forma que el resultado de la expresión n² + 2018nm + 2019m + n – 2019m² es un número primo?
Solución:
(more…)
Expresión compuesta
Problema 5 del viernes de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
¿Existen n y m naturales diferentes de cero de forma que el resultado de la expresión n² + 2018nm + 2019m + n – 2019m² es un número primo?

Solución: Aquí.
Solución a un primo en un triángulo rectángulo
Problema 4 del viernes de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
Sea p ≥ 3 un número primo, y consideremos el triángulo rectángulo de cateto mayor p² – 1 y cateto menor 2p.
Inscribimos en el triángulo un semicírculo cuyo diámetro se apoya en el cateto mayor y es tangente a la hipotenusa y al cateto menor del triángulo.
Encuentra los valores de p para los cuales el radio del semicírculo es un número entero.
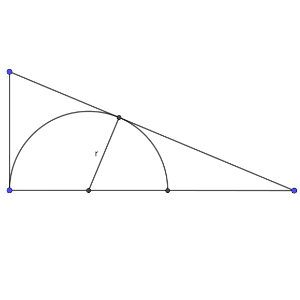
Solución: (more…)