Problema 1 de la Olimpiada Matemática Femenina Europea (EGMO 2018)
Se dirige a una edad de: 17 años
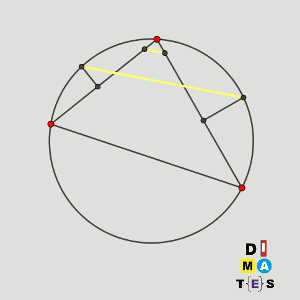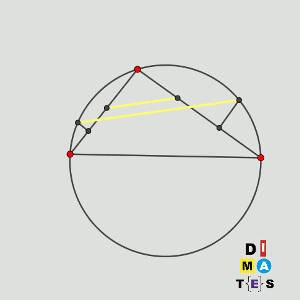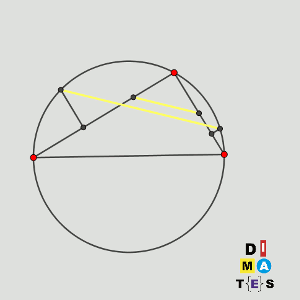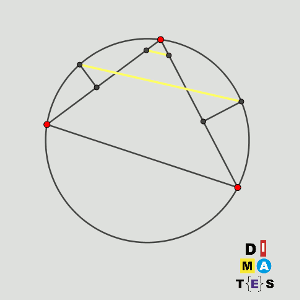
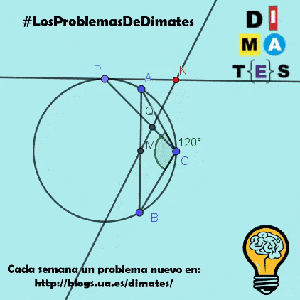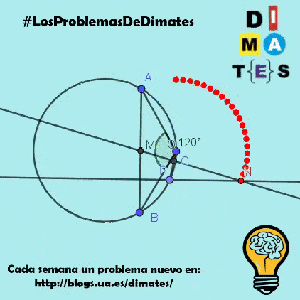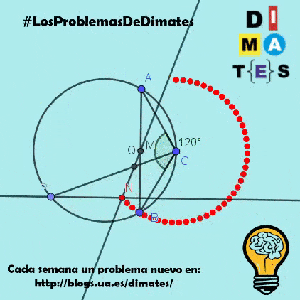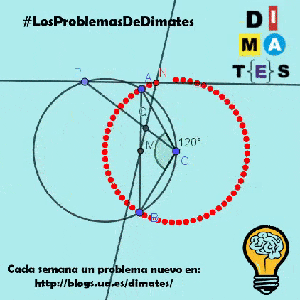
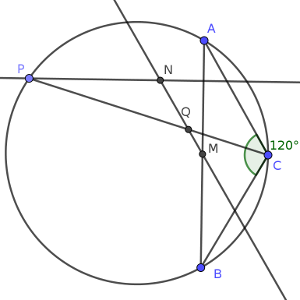
Sea ABC un triángulo de forma que CA = CB y el ángulo ACB mida 120º, y sea M el punto medio de AB.
Sea P un punto variable de la circunferencia que pasa por A, B y C.
Sea Q el punto en el segmento CP tal que QP = 2QC.
Se sabe que la recta que pasa por P y es perpendicular a la recta AB interseca a la recta MQ en un único punto N.
Demuestre que existe una circunferencia fija tal que N se encuentra en esa circunferencia para todas las posibles posiciones de P.
En esta ocasión se trata de un problema de construcción geométrica no demasiado complicado.
Lo más difícil es averiguar de qué circunferencia se trata la que contiene a N, y después todo consiste en demostrar que la distancia al centro de esa circunferencia siempre mide lo mismo.
Hay varias formas de abordar esto, pero a mí me gusta construir cuando es sencillo los problemas usando los vectores que se trabajan en bachillerato, aunque otros preferirán trabajar con propiedades geométricas. Sólo cuando se vuelve muy complejo el uso de vectores y ecuaciones busco aplicar otras reglas.
El triángulo ABC está perfectamente determinado excepto en su tamaño, así que lo voy a escalar y situar de forma que la circunferencia esté centrada en los ejes de coordenadas y (después de haber hecho un par de ensayos) me salgan la menor cantidad de fracciones posibles.
Para construir el triángulo con el ángulo de 120 grados, uso dos equiláteros unidos.
Al partir el triángulo equilátero en dos, aparecen dos triángulos rectángulos. Para que cumpla el Teorema de Pitágoras, si damos 6 unidades al lado del equilátero, uno de los catetos tendrá 3 y el otro raíz(27) = 3·raíz(3). Situando uno de los vértices del triángulo en (0, 0), las otras coordenadas serán (3, 3·raíz(3)) y las otras (6, 0).
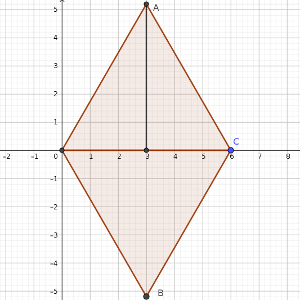
Para que el ángulo ACB sea de 120º, las coordenadas de A serán por lo tanto (3, 3·raíz(3)), B será (3, –3·raíz(3)) y C será (6, 0). Se puede comprobar que los tres puntos están sobre la circunferencia x² + y² = 36, es decir, que la distancia al (0, 0) siempre es 6.
Si aplicamos producto escalar, se pueden calcular los vectores CA y CB, multiplicarlos escalarmente y dividir por su módulo, y obtendremos el coseno del ángulo ACB, comprobando así que es –1/2, el que corresponde a 120º.
Es evidente que el punto medio entre A (3, 3·raíz(3)) y B (3, –3·raíz(3)), es M (3, 0).
Ahora, si tomamos un punto cualquiera P de la circunferencia, supondremos que sus coordenadas son (3a, 3b) (de nuevo, tomo variables de forma que sean múltiplo de 3, para poder dividir más tarde por 3 sin que salgan fracciones, en un primer borrador salían fracciones y he tomado esta decisión para simplificar). Debe cumplirse que 9a² + 9b² = 36 para que pertenezca a la circunferencia, es decir, que a² + b² = 4. Esto nos permitirá saber más adelante dónde está N.
Ahora vamos a calcular Q (en función de P). Puesto que QP = 2QC, como CQ + QP = CP, tendremos que CP = 3CQ, es decir, que si calculamos el vector CP, que es (3a – 6, 3b), lo multiplicamos por 1/3, obteniendo (a – 2, b) (para esto quería tanto múltiplo de 3), tendremos CQ. Ahora, C + CQ nos lleva a Q, es decir (6, 0) + (a – 2, b) = Q (a + 4, b).
Ya casi llegamos, vamos a calcular N. Puesto que AB es vertical, la recta PN es horizontal, es decir, la coordenada segunda (la y) de N es la misma que la de P, es decir, 3b. Para conocer la otra, una de las cosas que podemos hacer es obtener la ecuación de la recta MQ, y sustituir para encontrar la x, es decir, la coordenada horizontal. El vector MQ será (a + 1, b), y la ecuación de la recta tendrá entonces coeficientes de x e y, respectivamente, –b y a + 1. Es decir, que uno de los extremos de la ecuación será –bx + (a + 1)y, y el otro extremo será una constante. Como debe contener al punto M (3, 0), la constante debe ser –3b, así que la ecuación queda –bx + (a + 1)y = –3b. Ahora, sustituimos y por 3b, como hemos dicho, y tendremos –bx + (a + 1)3b = –3b, de donde, dividiendo por b, –x + (a + 1)3 = –3. Despejamos ahora x, y tenemos que 3 + (a + 1)3 = x, por lo que x = 3a + 6. El punto N, por tanto, será (3a + 6, 3b).
Ahora, vamos a ver si es cierto que N está siempre sobre una circunferencia. Nos ha quedado muy sencillo, ya que P (3a, 3b) está sobre una circunferencia, y N es (3a + 6, 3b). Es decir, que N está sobre una circunferencia 6 unidades a la derecha.
Normalmente, sería más complejo, ya que habría que ver, sabiendo la ecuación que cumple P, cuál cumple N, despejando y sustituyendo. Y saldría lo mismo, una circunferencia 6 unidades más a la derecha. Observa que el centro de la circunferencia original está en el (0, 0), por lo que el centro de la circunferencia de N está en (6, 0), que era nuestro C. Ahora que sabemos esto, podríamos retomar el problema buscando probar que la distancia de N a C es la misma sea cual sea P, lo que probablemente es más sencillo (aunque lo difícil es saber cuál es la circunferencia que buscamos).