Home » 2018 (Page 5)
Yearly Archives: 2018
Una lista que no termina en cero
Problema 1 del primer nivel de la Olimpiada de Mayo (2018) Se dirige a una edad de: 12 años
Juan hace una lista de 2018 números.
El primero es el 1. Luego, cada número se obtiene de sumarle al anterior alguno de los números 1, 2, 3, 4, 5, 6, 7, 8 o 9.
Sabiendo que ninguno de los números de la lista termina en cero, ¿cuál es el mayor valor que puede tener el último número de la lista?

Solución: Aquí.
Solución a juego con raíz de 5
Problema 4 de la Olimpiada Internacional (2018) Se dirige a una edad de: 17-19 años
Un lugar es un punto (x, y) en el plano tal que x e y son ambos enteros positivos menores o iguales que 20.
Al comienzo, cada uno de los 400 lugares está vacío.
Ana y Beto colocan piedras alternadamente, comenzando por Ana. En su turno, Ana coloca una nueva piedra roja en un lugar vacío tal que su distancia entre cualesquiera dos lugares ocupados por una piedra roja es distinto de la raíz de 5.
En su turno, Beto coloca una nueva piedra azul en cualquier lugar vacío (un lugar ocupado por una piedra azul puede estar a cualquier distancia de cualquier otro lugar ocupado).
Ellos paran cuando alguno de los dos no pueda colocar una piedra.
Halla el mayor k tal que Ana pueda asegurarse de colocar al menos K piedras rojas, sin importar cómo Beto coloque sus piedras azules.

Solución:
(more…)
Juego con raíz de 5
Problema 4 de la Olimpiada Internacional (2018) Se dirige a una edad de: 17-19 años
Un lugar es un punto (x, y) en el plano tal que x e y son ambos enteros positivos menores o iguales que 20.
Al comienzo, cada uno de los 400 lugares está vacío.
Ana y Beto colocan piedras alternadamente, comenzando por Ana. En su turno, Ana coloca una nueva piedra roja en un lugar vacío tal que su distancia entre cualesquiera dos lugares ocupados por una piedra roja es distinto de la raíz de 5.
En su turno, Beto coloca una nueva piedra azul en cualquier lugar vacío (un lugar ocupado por una piedra azul puede estar a cualquier distancia de cualquier otro lugar ocupado).
Ellos paran cuando alguno de los dos no pueda colocar una piedra.
Halla el mayor k tal que Ana pueda asegurarse de colocar al menos K piedras rojas, sin importar cómo Beto coloque sus piedras azules.
 Solución: Aquí.
Solución: Aquí.
Solución a dos paralelas en un círculo
Problema 1 de la Olimpiada Internacional (2018) Se dirige a una edad de: 17-19 años
Sea P la circunferencia circunscrita al triángulo acutángulo ABC. Los puntos D y E están en los segmentos AB y AC, respectivamente, y son tales que AD = AE. Las mediatrices de BD y CE cortan a los arcos menores AB y AC de P en los puntos F y G, respectivamente.
Demostrar que las rectas DE y FG son paralelas (o son la misma recta).
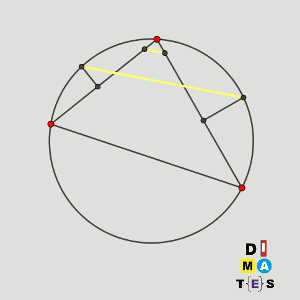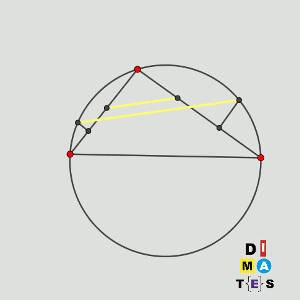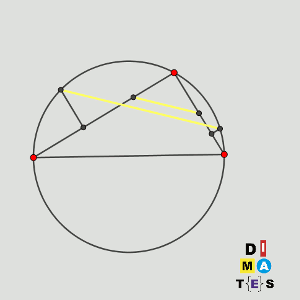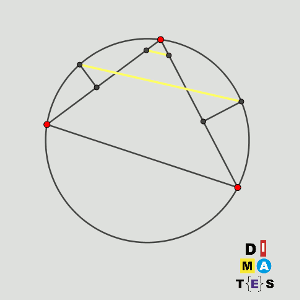
Solución:
(more…)
Dos paralelas en un círculo
Problema 1 de la Olimpiada Internacional (2018) Se dirige a una edad de: 17-19 años
Sea P la circunferencia circunscrita al triángulo acutángulo ABC. Los puntos D y E están en los segmentos AB y AC, respectivamente, y son tales que AD = AE. Las mediatrices de BD y CE cortan a los arcos menores AB y AC de P en los puntos F y G, respectivamente.
Demostrar que las rectas DE y FG son paralelas (o son la misma recta).

Solución a un juego justo
Problema 1 del reto de selección para el MathCamp de Estados Unidos y Canadá (2018) Se dirige a una edad de: 14-17 años
João y Kinga juegan a un juego con un dado justo de n caras, que están numeradas del 1 al n. En este juego, a João se le asigna un valor j y a Kinga un valor k, ambos en rango del 1 al n. João y Kinga se turnan lanzando el dado, empezando a lanzarlo João.
Si João obtiene un número menor o igual que j, el juego acaba y él gana. Si Kinga obtiene un número menor o igual que k, entonces gana Kinga y el juego acaba. El juego continúa hasta que uno de los dos jugadores gana.
Demuestra que si j = k, entonces João siempre tiene ventaja.
Si n = 6, encuentra todos los posibles valores de j y k que hacen el juego justo (es decir, que hacen que tanto João como Kinga tengan una probabilidad de un 50% de ganar).
Si n = 101, demuestra que ningún valor de j y k hacen el juego justo.
Solución:
(more…)
Un juego justo
Problema 1 del reto de selección para el MathCamp de Estados Unidos y Canadá (2018) Se dirige a una edad de: 14-17 años
João y Kinga juegan a un juego con un dado justo de n caras, que están numeradas del 1 al n. En este juego, a João se le asigna un valor j y a Kinga un valor k, ambos en rango del 1 al n. João y Kinga se turnan lanzando el dado, empezando a lanzarlo João.
Si João obtiene un número menor o igual que j, el juego acaba y él gana. Si Kinga obtiene un número menor o igual que k, entonces gana Kinga y el juego acaba. El juego continúa hasta que uno de los dos jugadores gana.
Demuestra que si j = k, entonces João siempre tiene ventaja.
Si n = 6, encuentra todos los posibles valores de j y k que hacen el juego justo (es decir, que hacen que tanto João como Kinga tengan una probabilidad de un 50% de ganar).
Si n = 101, demuestra que ningún valor de j y k hacen el juego justo.

Solución: Aquí.
Solución a números que contienen una suma
Problema 2 del segundo nivel de la Olimpiada de Mayo (2017) Se dirige a una edad de: 14 años
Varios números reales diferentes están escritos en la pizarra.
Si a, b y c son tres de estos números, al menos una de las siguientes sumas: a + b, a + c, b + c, también es uno de los números escritos en la pizarra.
¿Cuál es la mayor cantidad posible de números escritos en la pizarra?
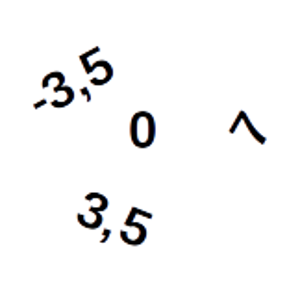
Solución:
(more…)
Números que contienen una suma
Problema 2 del segundo nivel de la Olimpiada de Mayo (2017) Se dirige a una edad de: 14 años
Varios números reales diferentes están escritos en la pizarra.
Si a, b y c son tres de estos números, al menos una de las siguientes sumas: a + b, a + c, b + c, también es uno de los números escritos en la pizarra.
¿Cuál es la mayor cantidad posible de números escritos en la pizarra?
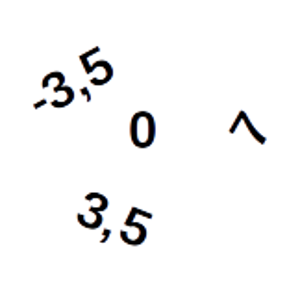
Solución: Aquí.
Solución a juego con dos colores
Problema 4 del primer nivel de la Olimpiada de Mayo (2017) Se dirige a una edad de: 12 años
Sea n un entero par mayor que 2.
Sobre los vértices de un polígono regular de n lados se pueden colocar fichas rojas o azules.
Dos jugadores, A y B juegan alternándose turnos del siguiente modo: cada jugador, en su turno, elige dos vértices que no tengan fichas y coloca en uno de ellos una ficha roja y en el otro una azul.
El objetivo de A es conseguir que haya tres vértices consecutivos con fichas del mismo color, mientras que el objetivo de B es impedir que esto suceda.
Al comienzo del juego no hay fichas en ninguno de los vértices.
Demostrar que, independientemente de quién empiece a jugar, el jugador B siempre podrá conseguir su objetivo.
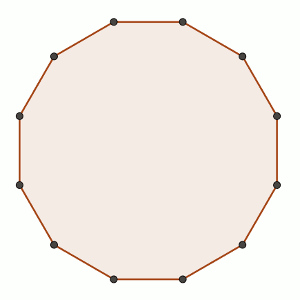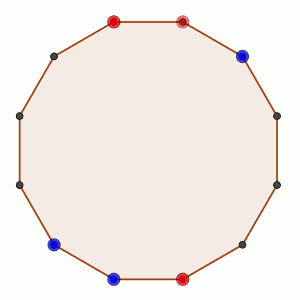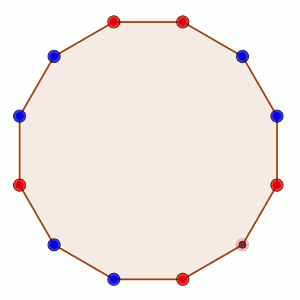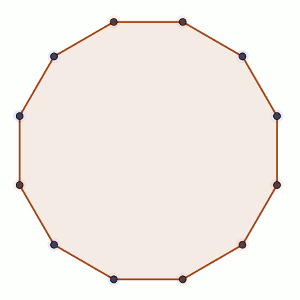
Solución:
(more…)