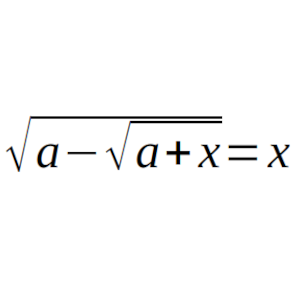Problema 3 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes)
Se dirige a una edad de: 16-17 años
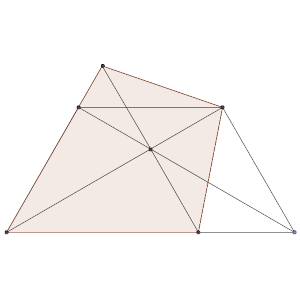
Sea ABCD un cuadrilátero.
Sean J e I los puntos medios de las diagonales AC y BD, respectivamente.
Sea G el punto de la recta BC tal que DG es perpendicular a BC y sea H el punto de la recta AD tal que CH es perpendicular a AD.
Las rectas DG y CH se cortan en el punto K.
Sea E el punto de la recta BC tal que AE es perpendicular a BC y sea F el punto de la recta AD tal que BF es perpendicular a AD.
Las rectas AE y BF se cortan en el punto L.
Probar que KL es perpendicular a JI.
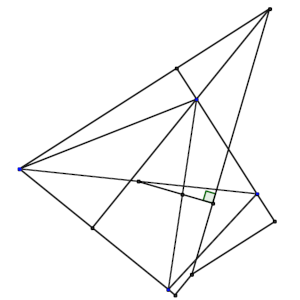
Solución: Aquí.