Problema 6 del concurso marató de problemes 2019 Se dirige a una edad de: 14-15 años
En un triángulo rectángulo ABC, la hipotenusa AC se divide en 12 partes iguales.
De cada una de ellas se traza una paralela al cateto BC, hasta el cateto AB, dividiendo el triángulo en 12 polígonos (un triángulo y 11 trapecios).
Hemos marcado dos de ellos, el cuarto a partir del vértice A, y el cuarto a partir del cateto BC.
¿Cuánto vale el resultado de dividir el área del mayor de los dos entre el otro?
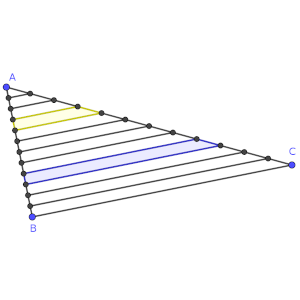
Soución
El área del triángulo es el producto de las dos longitudes de los catetos, a y c, entre 2 (ac/2).
Una forma directa de abordar el problema es ver cada zona como la diferencia de dos triángulos proporcionales al original.
Tal y como están trazados, cada triángulo de los que se forma guardará una proporción de razón x/12 con el original (el menor será 1/12, el segundo 2/12, etc.)
Así, sus áreas serán x²/144 del original, ya que esa proporcionalidad multiplica tanto al cateto a como al cateto c.
El ára amarilla, por tanto, será 16/144 del original menos 9/144 del original, es decir, 7/144 del original.
El área azul, por tanto, será 81/144 del original menos 64/144 del original, es decir, 17/144 del original.
El cociente, por tanto, será 17/7, una fracción irreducible.