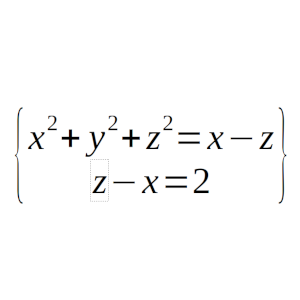Category: Olimpiada de la Comunidad Valenciana

Problema 3 del nivel A de la Fase Comarcal de la Olimpiada de la Comunidad Valenciana
Se dirige a una edad de: 12-13 años

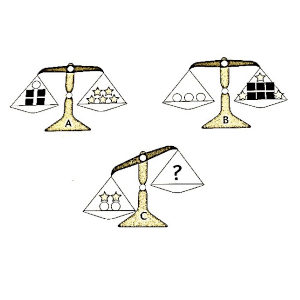
Tenemos una máquina que al introducirle un número en la casilla roja nos ofrece otro en la casilla azul.

El número de la casilla azul se transforma en otro que vemos en la casilla amarilla y, finalmente, el número de la casilla amarilla queda transformado en el que vemos en la casilla verde.

Hemos ido haciendo pruebas introduciendo números diferentes y viendo cómo se iban transformando. El problema es que el encargado de anotar los diferentes resultados lo ha hecho de pena, entre la mala letra que tiene y los que ha olvidado anotar, nos faltan varios.

¿Podrías completar la tabla?

Intenta obtener fórmulas para cada una de las casillas al introducir un número cualquiera R.

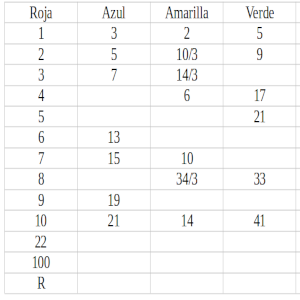
¿Cuál será la fórmula para ir directamente del número que introducimos en la casilla roja al obtenido en la verde? (por si no se viera la imagen, pongo a continuación una tabla)

Roja	Azul	Amarilla	Verde
1	3	2	5
2	5	10/3	9
3	7	14/3
4		6	17
5			21
6	13
7	15	10
8		34/3	33
9	19
10	21	14	41
22
100
R

Solución: Aquí.

Problema 2 del nivel B de la Fase Comarcal de la Olimpiada de la Comunidad Valenciana
Se dirige a una edad de: 14-15 años

Paula juega con tres palillos de la misma longitud.

Une dos de ellos formando una línea recta. El extremo del tercero lo coloca en el punto de unión de los dos anteriores.

Demuestra que si unes los tres extremos libres de los palillos, el triángulo que se dibuja siempre es un triángulo rectángulo, se coloque el tercer palillo como se coloque.

Solución: Aquí.

Problema 2 del nivel A de la Fase Comarcal de la Olimpiada de la Comunidad Valenciana
Se dirige a una edad de: 12-13 años

Roberta está practicando el salto de longitud.

La media de las distancias que saltó en los primeros intentos de hoy es de 3,80 m.

En su siguiente intento saltó 3,99, y su media subió hasta 3,81.

¿Qué distancia debe alcanzar en su siguiente salto para aumentar su media a 3,82?

Solución: Aquí.

Problema 1 del nivel C de la Fase Comarcal de la Olimpiada de la Comunidad Valenciana
Se dirige a una edad de: 10-11 años

Calcula las edades de cada uno de los cinco amigos Mariano, Laura, Reme, Paco y Mariola, que forman este grupo, teniendo en cuenta las siguientes condiciones:

Reme tiene 2 años menos que Paco.

Laura tiene 4 años más que Mariola, pero sólo uno más que Mariano.

Mariola nació en febrero de 2010 (hace 13 años).

Entre todos tienen 80 años.

¿Cuántos años han de pasar para que la suma de las edades de todos sea de 100 años?

Solución: Aquí.

Problema 1 del nivel B de la Fase Comarcal de la Olimpiada de la Comunidad Valenciana
Se dirige a una edad de: 14-15 años

Averigua el valor de x, y, y z en la expresión x² + y² + z² = x – z = 2.

Solución: Aquí.