Problema 1 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Hallar el menor entero positivo n tal que la suma de n sumandos
A(n) = 1 + 11 + 111 + … + 11…1
es divisible por 45.
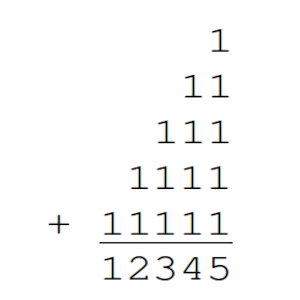
Solución:
Continue reading Solución a “Sumas de números formadas por unos”
Problema 4 del nivel A de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023 Se dirige a una edad de: 12 -13 años
En el cementerio de mi pueblo, hay una lápida en la que figura la siguiente inscripción: “Aquí yace Lucas Cuentas, muerto en 1971. Vivió tantos años como la suma de las cifras de su año de nacimiento”.
Calcula en qué año nació y cuánto vivió.
Problema 3 del nivel C de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023 Se dirige a una edad de: 10 -11 años
Un pequeño meteorito ha caído a la Tierra. Su impacto ha generado una zona de alta contaminación que abarca un cuadrado de 1 km de lado.
Los científicos de la Sociedad Geológica han prohibido que nadie se acerque a la zona a una distancia menor o igual a 1 km de cualquier punto contaminado.
a) Realiza el dibujo de la zona total no habitable delimitada por el perímetro decretado.
b) ¿Cuántos km2 son ahora inhabitables?
Solución:
Continue reading Solución a “Meteorito”
Problema 3 del nivel B de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023 Se dirige a una edad de: 14 -15 años
La figura se ha construido a partir de un triángulo equilátero de lado 2²⁰²² mediante la construcción sucesiva de triángulos equiláteros de lado la mitad del lado anterior.
Calcula el perímetro exterior de la figura, sabiendo que el lado del último triángulo dibujado es de longitud 2⁰ = 1.
Pista: 1 + 2 + 4 +… + 2^n = 2^(n + 1) – 1.
Solución:
Continue reading Solución a “Sucesión de triángulos”
Problema 2 del nivel C de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023 Se dirige a una edad de: 10 -11 años
Víctor y Sergio coleccionan los cromos de un álbum de fútbol. Una tarde comentan…
– Yo tengo el 92% de los cromos del álbum –dice Víctor-
– Y yo tengo 37, de cada 40 cromos del álbum –dice Sergio-
¿Quién tiene más cromos en el álbum? Justifica tu respuesta.
Continue reading Solución a “Cromos de fútbol”
Problema 1 del nivel C de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023 Se dirige a una edad de: 10 -11 años
Los alumnos de sexto han organizado una rifa para subvencionarse el viaje de fin de curso.
Y han decidido premiar, con un viaje gratis, todas las papeletas que den 21 al sumar las cifras del número que llevan impreso.
Las papeletas tienen impresos los números del 1 000 al 2 000.
¿Cuántas papeletas estarán premiadas?
Solución:
Continue reading Solución a “Viaje fin de curso”
Problema 3 del nivel A de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023 Se dirige a una edad de: 12 -13 años
Cada una de las dos mitades de la siguiente figura está compuesta por 22 triángulos pequeños, de los cuáles hay coloreados 4 de rojo, 6 de amarillo y 12 de verde.
Al doblar la figura por la recta AB resulta que quedan superpuestos tres pares de triángulos rojos, cuatro pares de amarillos y dos pares rojo/verde, no habiendo más parejas de estos tipos.
¿Cuántos pares de triángulos verdes coinciden?
Solución:
Continue reading Solución a “Emparejar triángulos”
Problema 2 del nivel B de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023 Se dirige a una edad de: 14 -15 años
Si el radio de la circunferencia mayor es 4 cm, calcula el área de la intersección de las dos circunferencias que muestra la figura.
Continue reading Solución a “Intersección de circunferencias”
Problema 2 del nivel A de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023 Se dirige a una edad de: 12 -13 años
Usando cuatro círculos iguales, de 4 cm de radio, hemos dibujado la flor que queda donde se solapan cada dos, tal y como se ve en el dibujo (la zona donde se superponen las marcas formando una cuadrícula).
Calcula el área que ocupa la flor.
Solución:
Continue reading Solución a “El área de la flor”
Problema 1 del nivel B de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2023 Se dirige a una edad de: 14 -15 años
En el rectángulo ABCD, de lados AB = 4 cm, y BC = 5 cm, se ha inscrito el cuadrilátero A’B’C’D’, haciendo que AA’ = BB’ = CC’ = DD’ = x.
Escribe la función que expresa el área de A’B’C’D’ en función de x.
¿Cuál es el dominio de la función?
¿Para qué valor de x se alcanza el mínimo?
Solución:
Continue reading Solución a cuadrilátero inscrito