Dada una función y = f(x), los puntos de su gráfica son (a, b) tal que b = f(a).
Como el eje de coordenadas vertical, Y, es el conjunto de puntos (0, y), entonces los puntos de la gráfica de y = f(x) que cortan a dicho eje son (0, f(0)).
Recordad que un número sólo puede tener una imagen y, como consecuencia, sólo hay una imagen de 0, f(0), y, por ende, un único punto (0, f(0)).
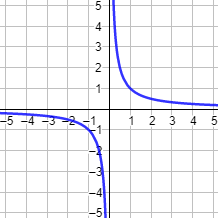
Ahora bien, puede darse el caso de que no existe la imagen de 0 por no ser éste un punto de su dominio. Por ejemplo, la función f(x) = 1/x no está definida para x = 0, puesto que no se puede dividir entre 0, por lo que dicha gráfica nunca corta al eje Y:
No ocurre lo mismo con el eje horizontal puesto que los puntos de la gráfica de y = f(x) que lo cortan son (a, 0) tales que f(a) = 0. Sí puede haber diferentes puntos del dominio cuya imagen sea 0 y podemos hallarlos resolviendo la ecuación f(x) = 0.
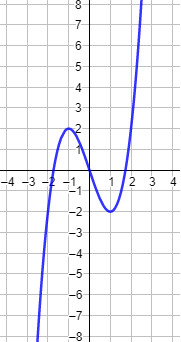
Por ejemplo, la gráfica de la función f(x) = x3-3x corta al eje vertical en tres puntos distintos:
Más información y temas relacionados:
- Cómo dibujar la gráfica de una función
- Dibujar gráficas de funciones
- Puntos de corte con los ejes
- Rectas y parábolas
- Dominio y recorrido
- Función continua
- Función inversa
- Asíntotas de funciones
- Problemas de funciones
- Funciones definidas a trozos
- Inyectiva y sobreyectiva
- Funciones pares e impares