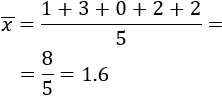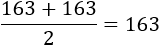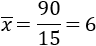Media
Dado un conjunto de datos, para calcular la media, se suman los datos y se divide el resultado entre el número de datos.
Ejemplo: el número de hermanos de un grupo de 5 niños es 1, 3, 0, 2 y 2.
Calculamos la media (sumamos el número de hermanos y dividimos entre 5):
La media es 1.6 hermanos.
Moda
La moda es el dato que más se repite.
En el ejemplo anterior el dato que más se repite es 2. Por tanto, la moda es 2.
Mediana
La mediana es el dato que ocupa la posición central, pero los datos deben estar ordenados.
Ordenamos los datos del ejemplo anterior: 0, 1 , 3, 2 y 2. El que ocupa la posición central es 3. Por tanto, la mediana es 3.
Si el número de datos es par, no hay uno que sea central. En este caso, se calcula la media de los dos datos centrales.
Ejemplo: las alturas de un grupo de 10 amigos son 155, 155, 159, 159, 163, 163, 170, 171, 172 y 178.
Los datos ya están ordenados y como hay 10 datos, los centrales son los de las posiciones 5 y 6, es decir, 163 y 163. La media de estos dos datos es 163.:
Por tanto, la mediana de las alturas es 163.
Ejemplo: Las notas del examen de matemáticas de 15 alumnos son las siguientes: 5, 3, 9, 7, 3, 6, 7, 5, 8, 7, 5, 4, 7, 6 y 8. Calcular la media, moda y mediana de las notas.
Para calcular la media, sumamos las notas y dividimos entre 15:
Ordenamos los datos de menor a mayor:
3, 3, 4, 5, 5, 5, 6, 6, 7, 7, 7, 7, 8, 8, 9
La moda es 7 (es la nota que más se repite).
Como hay 15 datos (número impar), la mediana es el dato de la posición 16/2 = 8. La mediana es 6.
Más información y temas relacionados: