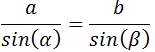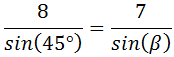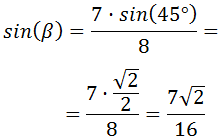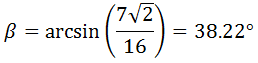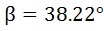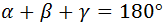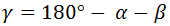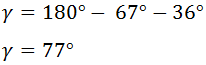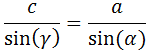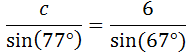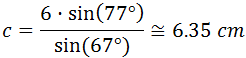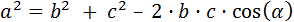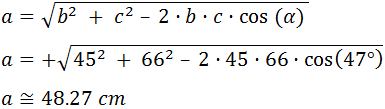El teorema del seno es un conocido e importante resultado de trigonometría que dice así:
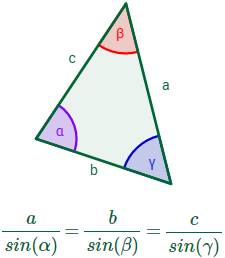
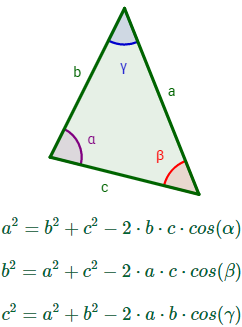
Sea un triángulo cualquiera con lados a, b y c y con ángulos interiores α, β y γ (son los ángulos opuestos a los lados, respectivamente). Entonces, se cumple la relación
Veamos dos ejemplos de aplicación:
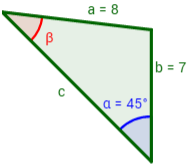
Ejemplo 1: en el siguiente triángulo de lados a = 8cm y b = 7cm. Calcular cuánto mide el ángulo β sabiendo que el ángulo γ mide 45º.
Como conocemos los lados a y b y el ángulo α, aplicamos el teorema del seno:
Por tanto,
Despejamos el seno de β:
Finalmente, despejamos β utilizando la inversa del seno (arcoseno):
Luego el ángulo es
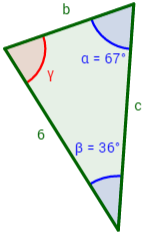
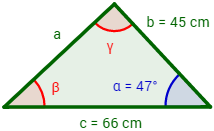
Ejemplo 2: se tiene un triángulo con ángulos α = 67° y β = 36° y un lado a = 6cm. ¿Cuánto mide el lado c?
Para calcular el lado c necesitamos conocer el ángulo γ.
Recordemos que en todo triángulo la suma de sus ángulos internos es 180°, es decir, tenemos la ecuación:
Despejamos el ángulo γ:
Sustituimos los valores:
Luego el ángulo es γ = 77º.
Ahora podemos aplicar el teorema del seno:
Sustituimos los datos:
Por tanto,
Luego el lado c mide 6.35 cm.
Más ejemplos y temas relacionados: