La regla de Barrow
Sea F(x) una función primitiva de la función f(x), es decir, la derivada de F(x) es f(x). Entonces, la regla de Barrow establece que la integral definida de f(x) en el intervalo [a, b] es F(b)-F(a):
Ejemplo: la función F(x) = x2 es una primitiva de la función f(x) = 2x. Por tanto, por la regla de Barrow, la integral definida de f(x) en el intervalo [0, 1] es
F(1) – F(0) = 12 – 02 = 1
Aplicaciones
La gran aplicación de la regla de Barrow es el cálculo del área que encierra la gráfica de una función con el eje de abscisas.
Supongamos, para simplificar los cálculos, que la función f(x) tiene su gráfica por encima del eje de abscisas para a ≤ x ≤ b:
Entonces, el área de la región encerrada entre la gráfica de f(x) y el eje de abscisas en el intervalo [a, b] es la integral definida de f(x) en [a, b], que por la regla de Barrow sabemos que es F(b)-F(a).
En el ejemplo anterior hemos calculado que el área encerrada por la gráfica de f(x) = 2x en [0, 1] es 1 .
Más información y temas relacionados:

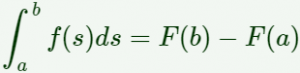
![la integral definida de f es el área de la región delimitada entre la gráfica de f, el eje OX en el intervalo [a,b] Issac Barrow (1630-1677): biografía, interpretación geométrica de la integral definida y demostración de la Regla de Barrow y del Teorema fundamental del cálculo](https://www.matesfacil.com/matematicos/Barrow/Barrow.png)