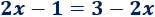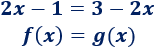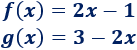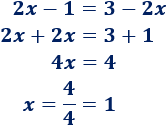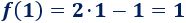Comúnmente, se considera la solución de una ecuación como el valor que debe tomar x para que la igualdad de la ecuación se cumpla. Sin embargo, podemos ver una ecuación como una igualdad entre dos funciones. Para que sea más sencillo de explicar y entender, nos ayudaremos de un ejemplo.
Recordad que la gráfica de una función f es el conjunto de puntos (x, f(x)). Teniendo esto en cuenta, si la gráfica de la función f y de la función g se cortan, lo hacen en un punto común (a, b) siendo b = f(a) = g(a).
Ejemplo
Sea la ecuación de primer grado
Consideremos esta ecuación como una igualdad entre dos funciones:
Lógicamente, las funciones f y g son
Como f(x) es la imagen de x mediante f y g(x) es la imagen de x mediante g, al igualar f(x) = g(x), estamos igualando las imágenes de x mediante f y g. Por tanto, la solución de la ecuación f(x) = g(x) son los valores que debe tomar x para que f(x) = g(x) y son, por ende, las primeras coordenadas de los puntos de corte entre las gráficas de f y g.
Resolvemos la ecuación del ejemplo:
Como la ecuación sólo tiene una solución, las gráficas de f y de g se cortan en un único punto: el punto cuya primera coordenada es x = 1. Calculamos la segunda coordenada de dicho punto:
Luego el punto de corte de las gráficas de f y de g es (1, 1).
Gráficas:
Al considerar una ecuación como una igualdad entre funciones para hallar sus puntos de corte, es fácil ver que pueden darse las siguientes situaciones:
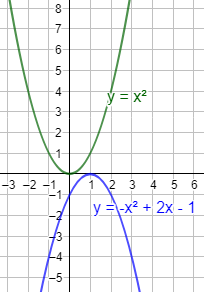
- Una ecuación puede no tener solución (real). Ocurre cuando las dos gráficas no se cortan:
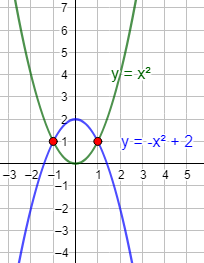
- Una ecuación puede tener una única solución. Ocurre cuando las dos gráficas se cortan en un único punto:
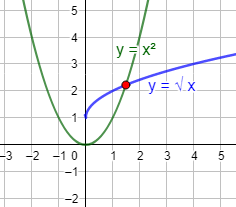
- Una ecuación puede tener varias soluciones. Ocurre cuando las dos gráficas se cortan en varios puntos:
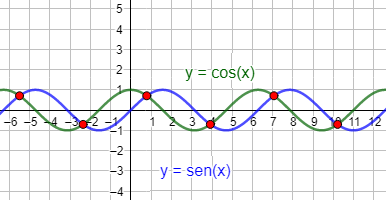
- Una ecuación puede tener infinitas soluciones. Ocurre cuando las dos gráficas son iguales (se cortan en todos sus puntos) o cuando se cortan en infinitos puntos pero no en todos:
Ahora bien, el número de soluciones dependerá de las funciones implicadas.
Más información y temas relacionados: