Las rectas son las funciones que tienen la siguiente forma:
donde m y n son números constantes:
- m es la pendiente de la recta
- n es la ordenada en el origen
La pendiente de una recta tiene cierta importancia puesto que nos informa de algunas propiedades de la recta. Por ejemplo,
- Si es positiva, la recta es creciente. Si es negativa, es decreciente.
- Si la pendiente es m = 0, entonces se trata de una recta constante, es decir, una recta horizontal paralela al eje de las abscisas.
- Cuanto mayor es |m|, mayor es el crecimiento/decrecimiento de la recta, es decir, cuanto mayor es |m|, más inclinada es la recta.
- Dos rectas con la misma pendiente son paralelas.
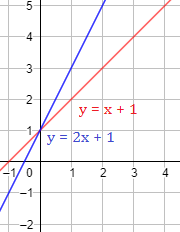
Ejemplo 1: gráficas de las rectas y = 2x + 1 (azul) e y = x + 1 (rojo)
Como las dos pendientes (m = 2 y m = 1) son positivas, las rectas son crecientes. Además, la que tiene mayor pendiente (azul) crece más rápido (está más inclinada).
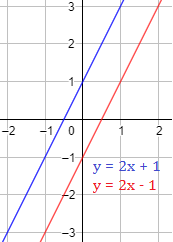
Ejemplo 2: gráficas de las rectas y = 2x + 1 (azul) e y = 2x – 1 (rojo)
Como ambas rectas tienen la misma pendiente (m = 2), son paralelas.
Más ejemplos y temas relacionados: