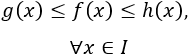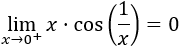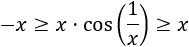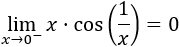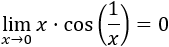El teorema del sándwich establece que si una función f(x) se encuentra entre dos funciones g(x) y h(x), es decir,
Y los límites de g(x) y de h(x) existen y son iguales, entonces el límite de f(x) también existe y coincide con el de g(x) y el de h(x).
Veamos un par de ejemplos de la importancia del teorema del sándwich en la práctica demostrando límites.
Ejemplo 1
En principio, este límite no es sencillo de calcular, puesto que la función seno es una función periódica que toma valores en el intervalo [-1, 1], por lo que el límite cuando x tiende a infinito es indeterminado.
Así, pues, vamos a acotar la función sin(x)/x entre dos funciones con límite.
Como el seno toma valores entre -1 y 1, podemos escribir
Dividimos entre x:
Ya tenemos la función acotada entre dos funciones (siempre que x sea mayor que 0) y estas funciones tienen límite cuando x tiende a infinito y es 0.
Por tanto, la función sin(x)/x también tiene límite y es 0:
Ejemplo 2
El coseno es una función periódica con valores en el intervalo [-1, 1], aunque existe su límite cuando x tiende a 0 y es cos(0) = 1. Sin embargo, en la función del límite el argumento del coseno es 1/x, el cual tiende a infinito cuando x tiende a 0. Además, el coseno del límite está además multiplicado por x.
A pesar de todo esto, el límite es sencillo de calcular mediante el teorema del sándwich. Acotamos el coseno:
Supongamos que x>0, entonces
Por el teorema del emparedado,
Ahora, hacemos lo mismo suponiendo que x<0:
Por el teorema del emparedado,
Como los límites laterales coinciden,
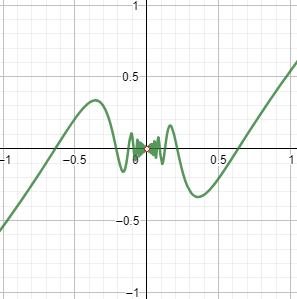
Gráfica de la función:
Más ejemplos en Teorema del emparedado o del sándwich.
Otros temas relacionados:
- Límites laterales
- 50 límites resueltos
- Más límites resueltos
- Introducción a las indeterminaciones
- Indeterminación infinito menos infinito
- Indeterminación 0 dividido 0
- Indeterminación infinito dividido infinito
- Indeterminación 0 por infinito
- Indeterminación 1 elevado a infinito
- Indeterminación 0 elevado a 0
- Indeterminación infinito elevado a 0
- Regla de l’Hôpital
- Infinitésimos equivalentes
- Límites de sucesiones