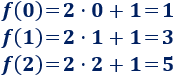La gráfica de una función matemática es su representación gráfica, la cual nos permite observar el comportamiento o propiedades de la misma. También, podemos obtener la imagen de un número a partir de la gráfica.
Recordamos que si y = f(x) es una función, entonces la imagen de un número a es b = f(a). Por ejemplo, consideremos la función f(x) = 2x + 1. Para calcular la imagen de un número, tenemos que sustituir x por dicho número:
Es decir,
- La imagen de 0 es 1.
- La imagen de 1 es 3.
- La imagen de 2 es 5.
Si a es un número y b es su imagen, es decir, b = f(a), entonces el punto (a, b) es un punto de la gráfica de f. Como hemos calculado varias imágenes, tenemos varios puntos:
- f(0) = 1 → tenemos el punto (0, 1).
- f(1) = 3 → tenemos el punto (1, 3).
- f(2) = 5 → tenemos el punto (2, 5).
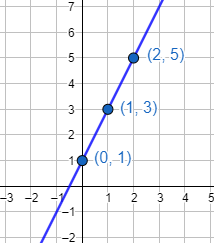
Si representamos estos puntos en el plano y los unimos, tenemos la gráfica de la función:
La gráfica de esta función es una recta.
Observando la gráfica, podemos deducir, por ejemplo, que la imagen de 3 es 7, es decir, f(3) = 7, ya que el punto (3, 7) está en la gráfica de f.
Como decíamos anteriormente, la gráfica permite observar el comportamiento de la función. Por ejemplo:
- La gráfica de esta función es una recta, pero las gráficas de las funciones también pueden ser curvas, por ejemplo.
- La recta es creciente (vista de izquierda a derecha), lo que significa que si a < b, entonces f(a) < f(b).
- Los puntos de corte con los ejes. Por ejemplo, la gráfica corta al eje Y en el punto (0, 1).
- Es una función continua, lo que significa que puede dibujarse de un solo trazo, lo cual no siempre es así.
Otros ejemplos de gráficas
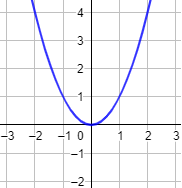
La gráfica de la función f(x) = x2 es una parábola (una curva):
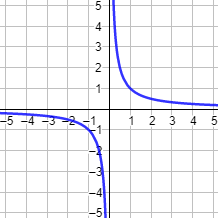
La gráfica de la función f(x) = 1/x NO es continua (tiene un salto):
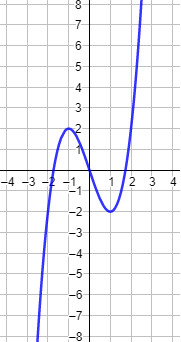
La gráfica de la función f(x) = x3 -3x es creciente, decreciente y creciente (de izquierda a derecha):
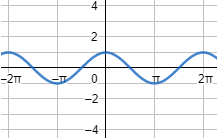
La gráfica de la función f(x) = cos(x) es periódica (se repite):
Otros temas relacionados: