Los cinco postulados de Euclides son 5 proposiciones no demostrables a partir de los cuales se fundamenta toda la geometría clásica. Fueron presentados en la obra Elementos, escrita 300 a. C.
Primer postulado
Por dos puntos distintos pasa una recta.
Representación gráfica:
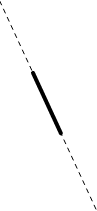
Segundo postulado
Un segmento rectilíneo puede prolongarse continuamente en una recta.
Representación gráfica:
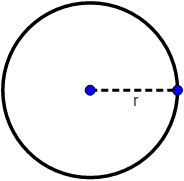
Tercer postulado
Hay una única circunferencia para cada centro y diámetro.
Representación gráfica:
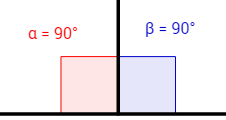
Cuarto postulado
Todos los ángulos rectos son iguales entre sí.
Representación gráfica:
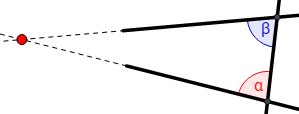
Quinto postulado
Al incidir una recta con otras dos, los ángulos internos del mismo lado son menores que el ángulo recto, las dos rectas, prolongadas indefinidamente, se encuentran en el lado en el cual los ángulos son menores que dos ángulos rectos.
Representación gráfica:
Este quinto postulado es mucho más complejo que los anteriores y, de hecho, suscitó polémica sobre si podía ser o no demostrado. Una versión equivalente y más sencilla de este postulado es:
Por un punto exterior a una recta pasa una única paralela.
Representación gráfica:
Más información y temas relacionados: