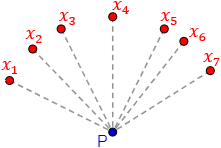
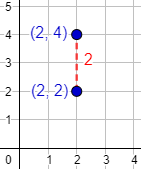
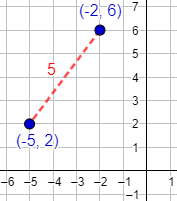
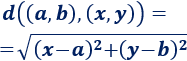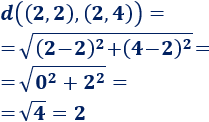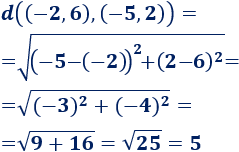Un punto P es equidistante de un conjunto de puntos x1, x2 … xn si la distancia de P a cada uno de estos puntos es la misma:
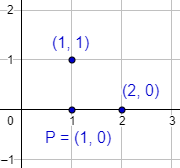
Ejemplo 1: El punto P = (0,1) es equidistante a los puntos x1 = (1, 1) y x2 = (2, 0):
La distancia de P a los puntos estos puntos es 1.
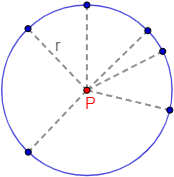
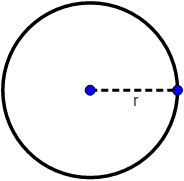
Ejemplo 2: los puntos de la circunferencia de radio r y centro P es un conjunto de puntos equidistantes de P:
La distancia de todos los puntos de la circunferencia a su centro es igual al radio, r.
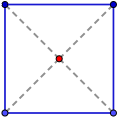
Ejemplo 3: en un cuadrado, los vértices equidistan del centro:
Observad que los vértices no son equidistantes entre sí.
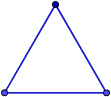
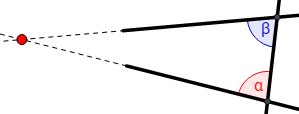
Ejemplo 4: en un triángulo equilátero, los vértices son equidistantes entre sí:
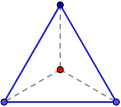
También, los vértices equidistan del ortocentro:
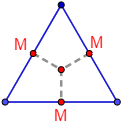
Y además, los puntos medios de cada lado equidistan del ortocentro:
Nota: el ortocentro es el punto donde intersectan las tres alturas del triángulo.
Más ejemplos y temas relacionados: