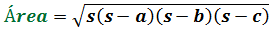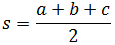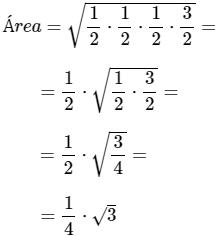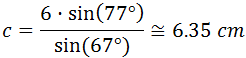Tag: triángulo

Posted on

Fórmula de Herón

Seguramente la fórmula más utilizada para calcular el área, A,  de un triángulo cualquiera de altura h y base b es

Herón de Alejandría: biografía y la fórmula y el método de Herón (área de un triángulo y aproximación de raíces cuadradas)

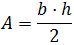
Sin embargo, disponemos también de otra sencilla fórmula que se utiliza con menos frecuencia, la cual es función de la longitud de los lados del triángulo en lugar de su base y altura: la fórmula de Herón.

Fórmula de Herón

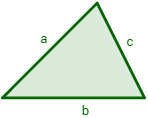
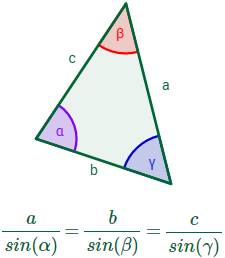
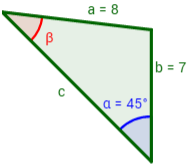
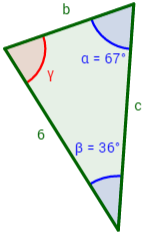
Dado un triángulo de lados a, b y c

Herón de Alejandría: biografía y la fórmula y el método de Herón (área de un triángulo y aproximación de raíces cuadradas)

Entonces, su área es

Herón de Alejandría: biografía y la fórmula y el método de Herón (área de un triángulo y aproximación de raíces cuadradas)

siendo s su semiperímetro, que es la mitad de la suma de sus lados:

Herón de Alejandría: biografía y la fórmula y el método de Herón (área de un triángulo y aproximación de raíces cuadradas)

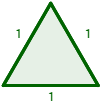
Ejemplo: calculamos el área del triángulo equilátero de lado 1:

Herón de Alejandría: biografía y la fórmula y el método de Herón (área de un triángulo y aproximación de raíces cuadradas)

Como el triángulo es equilátero, sus tres lados miden lo mismo: 1. Por tanto, su perímetro es 3 y su semiperímetro es 2/3:

Calculamos el área:

 

Más información y temas relacionados:

 

Posted on

Semiperímetro

El perímetro de un polígono es la suma de todos sus lados.

El semiperímetro de un polígono es la mitad de su perímetro.

Aunque sea un concepto aparentemente poco útil, tiene algunas aplicaciones, razón por la que debemos conocerlo. Por ejemplo, el semiperímetro se utiliza para calcular el área de un triángulo mediante la fórmula de Herón.

Ejemplo 1

Herón de Alejandría: biografía y la fórmula y el método de Herón (área de un triángulo y aproximación de raíces cuadradas)

El perímetro de una triángulo equilátero cuyos lados miden 1 es 3. Por tanto, el semiperímetro es 1,5.

 

Ejemplo 2

Problemas resueltos de tetrágonos regulares (cuadrados): calcular perímetro, área y diagonales. Polígonos. Geometría plana. Secundaria.

El perímetro de un cuadrado de lado 4cm es 16cm. Por tanto, su semiperímetro es 8cm.

 

Ejemplo 3

Problemas resueltos de pentágonos regulares: calcular perímetro, área, apotema, demostrar la fórmula del área, etc. Polígonos. Secundaria.

El perímetro de un pentágono regular de lado 1,5 es 7,5. Por tanto, su semiperímetro es 3,75.

 

Ejemplo 4

El perímetro de un hexágono regular de lado 2 es 12. Por tanto, su semiperímetro es 6.

 

Temas relacionados:

Posted on

Teorema del seno

El teorema del seno es un conocido e importante resultado de trigonometría que dice así:

Sea un triángulo cualquiera con lados a, b y c y con ángulos interiores α, β y γ (son los ángulos opuestos a los lados, respectivamente). Entonces, se cumple la relación

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Veamos dos ejemplos de aplicación:

Ejemplo 1: en el siguiente triángulo de lados a = 8cm y b = 7cm. Calcular cuánto mide el ángulo β sabiendo que el ángulo γ mide 45º.

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Como conocemos los lados a y b y el ángulo α, aplicamos el teorema del seno:

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Por tanto,

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Despejamos el seno de β:

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Finalmente, despejamos β utilizando la inversa del seno (arcoseno):

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Luego el ángulo es

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Ejemplo 2: se tiene un triángulo con ángulos α = 67° y β = 36° y un lado a = 6cm. ¿Cuánto mide el lado c?

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Para calcular el lado c necesitamos conocer el ángulo γ.

Recordemos que en todo triángulo la suma de sus ángulos internos es 180°, es decir, tenemos la ecuación:

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Despejamos el ángulo γ:

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Sustituimos los valores:

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Luego el ángulo es γ = 77º.

Ahora podemos aplicar el teorema del seno:

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Sustituimos los datos:

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Por tanto,

el teorema del seno (con demostración) y problemas resueltos de su aplicación: calcular lados, ángulos y áreas de triángulos. Fórmula del área de un triángulo aplicando el teorema del seno.

Luego el lado c mide 6.35 cm.

Más ejemplos y temas relacionados: