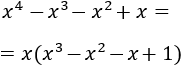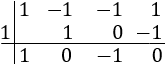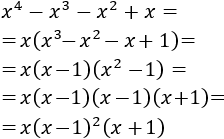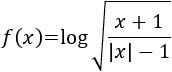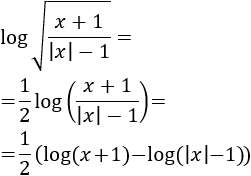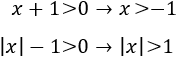Vimos en continuidad de funciones que una una función con una raíz cuadrada es continua en los reales para los que el radicando es no negativo. A continuación vamos a ver algunos ejemplos.
Ejemplo 1
Tenemos que buscar los puntos para los cuales el radicando es es positivo.
Igualamos el radicando a 0 y resolvemos la ecuación:
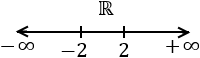
Estas dos soluciones dividen la recta real en tres intervalos:
En uno o dos de estos intervalos, el radicando de la función es no negativo. Para saber cuál es, sólo tenemos que escoger algún punto al azar de cada intervalo.
Primer intervalo:
Segundo intervalo:
Tercer intervalo:
Por tanto, el radicando es no negativo en el primer y tercer intervalo. Luego la función es continua en
Observad que incluimos los puntos x=2 y x=-2 porque para estos valores el radicando es 0.
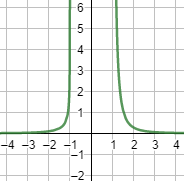
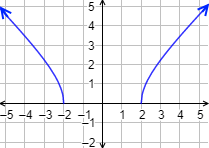
Gráfica:
Ejemplo 2
- El radicando de la raíz debe ser no negativo.
- El denominador tiene que ser distinto de 0.
Igualamos el radicando a 0:
Hay que estudiar el signo del radicando los intervalos siguientes:
Dando valores, el radicando es no negativo en el primer y tercer intervalo.
Factorizamos el denominador:
Aplicamos la regla de Ruffini para hallar las soluciones del polinomio de tercer grado:
Por tanto,
Tenemos que excluir los puntos 0, 1 y -1.
El dominio es el conjunto de los reales excepto el intervalo [-1, 1]. La función es continua en su dominio.
Gráfica:
Ejemplo 3
- El argumento del logaritmo debe ser positivo.
- El radicando debe ser no negativo.
- El denominador debe ser no nulo.
Aplicando las propiedades de los logaritmos,
De este modo, es fácil ver que deben cumplirse las siguientes inecuaciones:
Se cumplen ambas sólo si x>1.
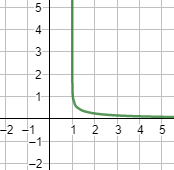
Así, pues, el dominio de la función es ]1, +∞[. La función es continua en su dominio.
Gráfica:
Más ejemplos en

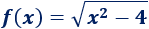
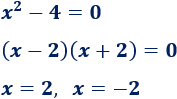
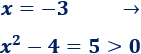
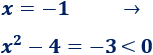
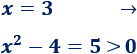
![unión de los intervalos (-∞, -2] y [2,+∞) Definimos función continua y discontinua, mostramos algunos ejemplos y resolvemos 5 problemas. Funciones polinómicas, funciones racionales, funciones definidas a trozos, funciones con raíces y funciones trigonométricas. ESO y Bachillerato. Matemáticas. Continuidad de funciones.](https://www.problemasyecuaciones.com/funciones/continua/P2-5.png)
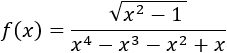
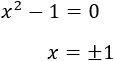
![intervalos ]-∞-1[, ]-1,1[ y ]1,+∞[ Explicamos el concepto de continuidad de una función (especialmente en el caso de las funciones continuas, por lo que usamos límites laterales). Proporcionamos ejemplos y resolvemos ejercicios de calcular el dominio y la continuidad. Ejercicios resueltos. Matemáticas. Bachillerato. Análisis.](https://www.matesfacil.com/BAC/continuidad/conti6-2b.png)