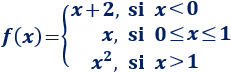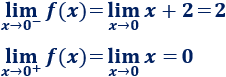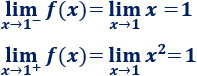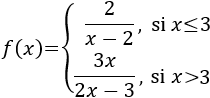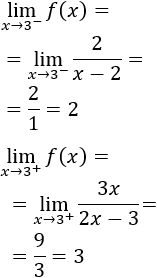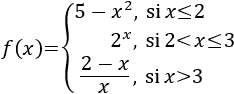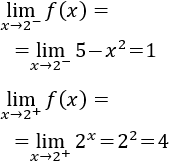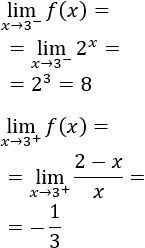La continuidad de una función definida a trozos o por intervalos se estudia del mismo que una función normal, pero hay que tratar los puntos donde cambia la definición de la función como posibles puntos de discontinuidad. En estos puntos, tenemos que comprobar si los límites laterales coinciden.
Veamos algunos ejemplos.
Ejemplo 1
La función es continua en cada uno de los tres intervalos puesto que se tratan de polinomios. Los posibles candidatos a puntos de discontinuidad son los extremos de los intervalos: x=0 y x=1.
Calculamos los límites laterales en estos puntos:
Punto x=0
Punto x=1
El único punto de discontinuidad es x=0, ya que los límites laterales no coinciden.
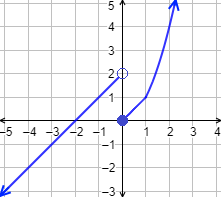
Gráfica:
Ejemplo 2
- En el intervalo x≤3, la función es racional. Tenemos que excluir el punto x=2 del dominio porque anula al denominador.
- En el intervalo x>3, también es racional. El denominador se anula en x=3/2 <3, así que no hay que excluir ningún punto.
El dominio de la función es el conjunto de los reales excepto x=2.
Calculamos los límites laterales en el punto x=3:
Como no coinciden, la función no es continua en x=3.
La función es continua en todos los reales excepto en x=2 y x=3.
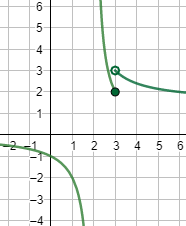
Gráfica:
Ejemplo 3
El dominio es el conjunto de los reales.
En cada intervalo (abierto) de definición, la función es continua. Tenemos que ver qué ocurre en los puntos x=2 y x=3.
Límites laterales en x=2:
Como los límites son distintos, no hay continuidad en x=2.
Límites laterales en x=3:
Como los límites son distintos, no hay continuidad en x=3.
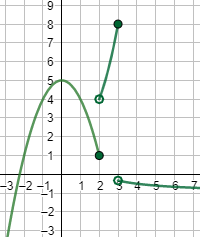
Por tanto, la función es continua en el conjunto de los reales excepto en x=2 y x=3.
Gráfica:
Más ejemplos y temas relacionados: