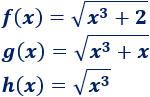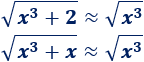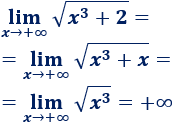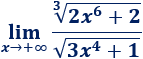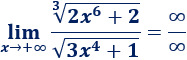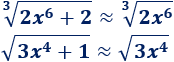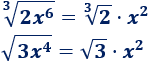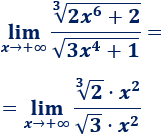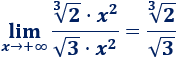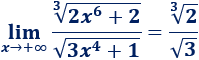Anteriormente, vimos cómo calcular el límite de una raíz. En este post explicamos cómo calcular límites de fracciones de raíces.
La técnica que usaremos es omitir los sumandos irrelevantes de los radicandos.
Supongamos que tenemos las siguientes funciones que son raíces cuadradas de polinomios de tercer grado:
Los límites dependen de los monomios de grado mayor (en nuestro caso, es el monomio x3). Esto de sebe a que estos monomios son los que más peso tienen en la suma cuando x toma valores muy grandes (o muy pequeños).
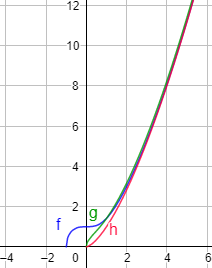
Como las tres funciones tienen un polinomio del mismo grado (grado 3), su comportamiento es similar cuando x toma valores grandes, como se observa en sus gráficas:
Podríamos decir que las funciones son casi iguales:
Esto nos facilita el cálculo de límites: los tres límites de estas funciones coinciden:
Importante: no hay que aplicar este procedimiento cuando tenemos una resta de raíces.
A continuación, explicamos cómo aplicar la técnica anterior para calcular límites de cocientes de raíces.
Supongamos que tenemos un cociente de raíces de distinto orden:
Cuando x tiende a +∞, los radicandos tienden a infinito y, por tanto, tenemos un cociente de infinitos:
Sin embargo, podemos cambiar las raíces por raíces casi iguales, según vimos anteriormente:
Además, podemos aplicar las propiedades de las raíces/potencias:
Por tanto, podemos ver el límite inicial como un cociente de polinomios:
Recordad que el límite del cociente de dos polinomios del mismo grado es igual al cociente de sus coeficientes principales:
Por tanto,
Más información y ejemplos:
- Límites de raíces
- Límites de funciones exponenciales
- Límites resueltos
- 50 límites resueltos
- Indeterminación 1 elevado a infinito
- Otros temas de límites