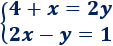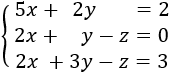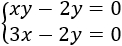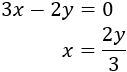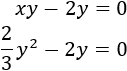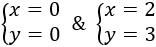Las ecuaciones de un sistema de ecuaciones lineales tienen las incógnitas separadas en monomios distintos y sin exponentes.
Ejemplo 1: sistema de 2 ecuaciones lineales con 2 incógnitas (x e y):
Ejemplo 2: sistema de 3 ecuaciones lineales con 3 incógnitas (x, y y z):
Existen métodos básicos para resolver los sistemas de ecuaciones lineales:
Y algunos métodos más avanzados del álgebra matricial:
Sistema de ecuaciones NO lineales
Cuando las ecuaciones no son lineales, la resolución del sistema es más compleja. Generalmente, no existe un método concreto para resolverlo, debido a la diversidad de las ecuaciones implicadas.
Ejemplo 3: sistema de 2 ecuaciones con 2 incógnitas:
La primera ecuación no es lineal porque las incógnitas aparecen multiplicadas entre sí. La segunda ecuación sí es lineal.
En este caso en concreto, podemos resolver el sistema por sustitución.
Despejamos la x en la segunda ecuación:
Sustituimos en la primera ecuación:
Tenemos una ecuación de segundo grado cuyas soluciones son y = 0 e y = 3. Sustituimos en la ecuación x = 2y/3 para obtener x = 0 y x = 2. Por tanto, este sistema de ecuaciones tiene dos soluciones distintas:
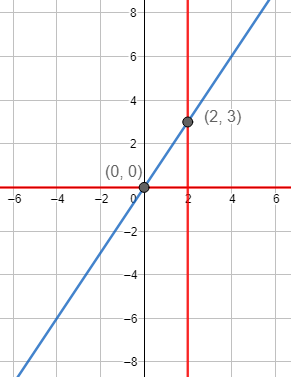
Gráfica: si representamos las dos ecuaciones, las dos soluciones son los puntos de intersección:
Más ejemplos y temas relacionados: