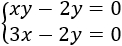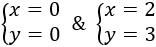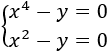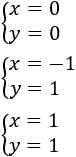Recordad que el Teorema de Rouché-Frobenius establece que un sistema de ecuaciones lineales puede:
- No tener solución (sistema incompatible).
- Tener una única solución (sistema compatible determinado).
- Tener infinitas soluciones (sistema compatible indeterminado).
No ocurre lo mismo con los sistemas de ecuaciones NO lineales, puesto que también puede darse el caso de que tengan un número finito de soluciones distintas, como mostramos en los dos siguientes ejemplos.
Ejemplo 1: sistema de 2 ecuaciones (una no lineal y otra lineal) con dos incógnitas:
Este sistema tiene dos soluciones distintas:
Ejemplo 2: sistema de 2 ecuaciones no lineales con dos incógnitas:
Este sistema tiene 3 soluciones distintas:
Lógicamente, el número de soluciones está relacionado con el tipo de ecuaciones implicadas en el sistema, pero sería difícil establecer una regla genérica. Cada sistema de ecuaciones no lineales es un caso especial.
La resolución de los sistemas anteriores podéis encontrarla en: sistemas de ecuaciones no lineales.
Temas relacionados: