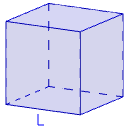
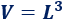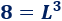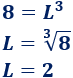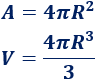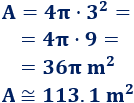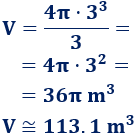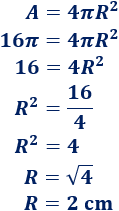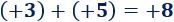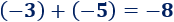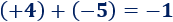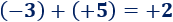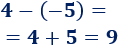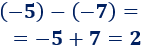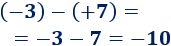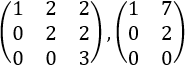Posts

Posted on

Área y volumen del cubo

El cubo es el poliedro regular de 6 caras cuadradas.

Proporcionamos una calculadora online y las fórmulas de un cubo de arista L. Con ejemplos, representaciones y problemas resueltos. Geometría tridimensional. Geometría 3D. Secundaria. ESO. Matemáticas.

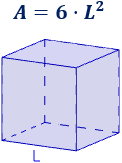
Área del cubo

El área del cubo de arista L es

Proporcionamos una calculadora online y las fórmulas de un cubo de arista L. Con ejemplos, representaciones y problemas resueltos. Geometría tridimensional. Geometría 3D. Secundaria. ESO. Matemáticas.

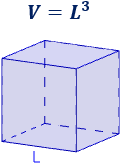
Volumen del cubo

El volumen del cubo de arista L es

Proporcionamos una calculadora online y las fórmulas de un cubo de arista L. Con ejemplos, representaciones y problemas resueltos. Geometría tridimensional. Geometría 3D. Secundaria. ESO. Matemáticas.

Ejemplo: ¿Cuánto mide la arista de un cubo cuyo volumen es 8 centímetros cúbicos?

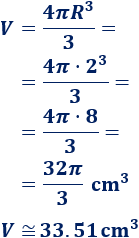
La fórmula del volumen del cubo de arista L es

Proporcionamos una calculadora online y las fórmulas de un cubo de arista L. Con ejemplos, representaciones y problemas resueltos. Geometría tridimensional. Geometría 3D. Secundaria. ESO. Matemáticas.

Como sabemos que el volumen es V = 8, tenemos la ecuación

Proporcionamos una calculadora online y las fórmulas de un cubo de arista L. Con ejemplos, representaciones y problemas resueltos. Geometría tridimensional. Geometría 3D. Secundaria. ESO. Matemáticas.

Para calcular L, tenemos que hacer la raíz cúbica:

Proporcionamos una calculadora online y las fórmulas de un cubo de arista L. Con ejemplos, representaciones y problemas resueltos. Geometría tridimensional. Geometría 3D. Secundaria. ESO. Matemáticas.

La raíz cúbica de 8 es 2 porque 23 es 8.

Luego la arista del cubo mide 2 centímetros.

Más ejemplos y temas relacionados:

Posted on

Área y volumen de la esfera

Una esfera de radio R y centro P es el conjunto de puntos del espacio que distan R del punto P:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

Área (A) y volumen (V) de la esfera de radio R

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

Ejemplo 1: calcular el área y el volumen de un esfera de radio R = 3 metros.

Sólo tenemos que sustituir en las fórmulas.

Calculamos el área:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

Calculamos el volumen:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

Los resultados coinciden, pero el área es en metros cuadrados y el volumen es en metros cúbicos.

Ejemplo 2: Si el área de una esfera es A = 15π cm2 ¿Cuál es su volumen?

Usamos la fórmula del área para calcular el radio:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

Ahora que conocemos el radio, podemos calcular el volumen:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

El volumen es, aproximadamente, 33.51 cm3.

Más ejemplos y temas relacionados:

Posted on

Suma y resta de enteros

Suma de números enteros

Si los dos enteros a sumar tienen el mismo signo, se suman los números (sin signo) y se conserva el signo.

Ejemplo 1

Sumamos los enteros +3 y +5:

Explicamos las operaciones básicas con números enteros (suma, resta, multiplicación y división) y proporcionamos algunos ejemplos y ejercicios de operaciones combinadas. ESO. Álgebra básica. Matemáticas.

Sumamos los enteros -3 y -5:

Explicamos las operaciones básicas con números enteros (suma, resta, multiplicación y división) y proporcionamos algunos ejemplos y ejercicios de operaciones combinadas. ESO. Álgebra básica. Matemáticas.

Si los dos enteros tienen signos distintos, se restan los números (sin signo) y se conserva el signo del número que sea mayor (sin signo).

Ejemplo 2

Sumamos los enteros +4 y -5:

Explicamos las operaciones básicas con números enteros (suma, resta, multiplicación y división) y proporcionamos algunos ejemplos y ejercicios de operaciones combinadas. ESO. Álgebra básica. Matemáticas.

Sumamos los enteros -3 y +5:

Explicamos las operaciones básicas con números enteros (suma, resta, multiplicación y división) y proporcionamos algunos ejemplos y ejercicios de operaciones combinadas. ESO. Álgebra básica. Matemáticas.

Resta de números enteros

Cuando tenemos una resta de enteros, podemos transformarla en una suma cambiando el signo del segundo sumando.

Ejemplo 4

Restamos los enteros 4 y -5:

Explicamos las operaciones básicas con números enteros (suma, resta, multiplicación y división) y proporcionamos algunos ejemplos y ejercicios de operaciones combinadas. ESO. Álgebra básica. Matemáticas.

Restamos los enteros -5 y -7:

Explicamos las operaciones básicas con números enteros (suma, resta, multiplicación y división) y proporcionamos algunos ejemplos y ejercicios de operaciones combinadas. ESO. Álgebra básica. Matemáticas.

Restamos los enteros -3 y 7:

Explicamos las operaciones básicas con números enteros (suma, resta, multiplicación y división) y proporcionamos algunos ejemplos y ejercicios de operaciones combinadas. ESO. Álgebra básica. Matemáticas.

Más ejemplos y temas relacionados:

Posted on

Matriz triangular

Sea A una matriz de dimensión mxn,

  • Es una matriz triangular superior si tiene 0’s por debajo de la diagonal, es decir, si aij=0 para i>j. Por ejemplo,

    Clasificación de las matrices según su forma en identidad, diagonal, bidiagonal, tridiagonal, triangular, traspuesta, adjunta, simétrica, antisimétrica, definida positiva, diagonalmente dominante, Hessenberg y Vandermonde. Con propiedades y ejemplos. Álgebra matricial. Matrices.

  • Es una matriz triangular inferior si tiene 0’s por encima de la diagonal, es decir, si aij=0 para i<j.

Por ejemplo,

Clasificación de las matrices según su forma en identidad, diagonal, bidiagonal, tridiagonal, triangular, traspuesta, adjunta, simétrica, antisimétrica, definida positiva, diagonalmente dominante, Hessenberg y Vandermonde. Con propiedades y ejemplos. Álgebra matricial. Matrices.

Posted on

Sistema de numeración posicional

Los sistemas de numeración son posicionales cuando el valor del cada dígito del número depende de la posición en la que se encuentra.

Ejemplos de sistemas posicionales: binario, quinario, decimal, octal y hexadecimal. Un ejemplo de sistema de numeración no posicional es el sistema romano.

Símbolos del sistema

Cada sistema utiliza sus propios símbolos:

  • Decimal: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9.
  • Binario: 0 y 1.
  • Quinario: 0, 1, 2, 3 y 4.
  • Octal: 0, 1, 2, 3, 4, 5, 6 y 7.
  • Hexadecimal: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E y F.

Conversión

Para pasar un número en sistema decimal o cualquiera de los otros sistemas citados, se calcula una serie de divisiones (entre la base) y el número en la nueva base (escrito de derecha a izquierda) es el último cociente obtenido seguido de todos los restos obtenidos.

Ejemplo: el número en decimal 768 es el número 1400 en octal.

La conversión inversa, es decir, para pasar al sistema decimal, se suma el resultado de cada dígito multiplicado por la potencia n-ésima de la base, siendo n la posición del dígito (de derecha a izquierda y comenzando por 0). En el caso del sistema hexadecimal, los símbolos A, B, C, D, E y F representan 10, 11, 12, 13, 14, y 15, respectivamente.

Ejemplo: el número en hexadecimal A37F es el número 41855 en decimal.

Recursos: 

Posted on

Eugène Rouché

Eugène Rouché (1832 –1910) fue un matemático francés, profesor de esta ciencia en el liceo Charlemagne y posteriormente en la École Centrale.

Rouché es conocido, sobre todo, por el Teorema de Rouché de análisis complejo sobre funciones holomorfas publicado en 1862.

Otro de sus resultados más conocidos es el teorema de Rouché-Frobenius que relaciona los rangos de las matrices de coeficientes y ampliada de la representación matricial de un sistema de ecuaciones lineales con el tipo de soluciones de éste.

El matemático coetáneo Georges Fontené (1848-1923) reclamó la autoría de la demostración del teorema de Rouché-Frobenius y más tarde, en 1905, el matemático alemán Ferdinand Georg Frobenius (1849-1917) acreditó la autoría tanto a Rouché como a Fontené.

Otros matemáticos:

Posted on

¿Para qué sirven las Ecuaciones?

Escribimos este post ya que muchos estudiantes se preguntan para qué aprender a resolver ecuaciones. Un ejemplo de la utilidad de las ecuaciones es la resolución de problemas que aparecen en nuestra vida cotidiana.

Veamos un ejemplo de problema práctico:

Problema

Queremos diseñar una habitación de 18 metros cuadrados con forma rectangular de modo que el largo de la misma sea el doble que el ancho.

Solución

  • Llamamos x al ancho de la habitación.
  • Como el largo tiene que ser el doble del ancho, el largo es 2·x. 
  • El área de un rectángulo es el producto del ancho por el largo:

Área = x·2·x = 2·x2

Como el área tiene que ser 18, tenemos la ecuación

18 =2·x2

La ecuación que tenemos es una ecuación de segundo grado incompleta. Esta ecuación tiene dos soluciones: x = 3 y x = -3. 

La solución del problema es la solución positiva porque la incógnita x representa una longitud.

Por tanto, el largo de la habitación debe ser 6 metros y el ancho debe ser 3 metros. El área es 3·6 = 18 m2.

 

¡Ahora ya no tenéis excusa para pensar que las ecuaciones no sirven para nada!

Más ejemplos de problemas prácticos:

Posted on

Contacto

Esta página web contiene algunas imágenes y problemas de otras páginas web bajo su consentimiento.

Si detectas algún error o quieres contactar por otra razón, puedes hacerlo a través de los comentarios en este post. El comentario no será visible.

Posted on

¿Hay ecuaciones sin solución?

La respuesta a la pregunta ¿hay ecuaciones sin solución? es que sí:

No todas las ecuaciones tienen solución.

 

Veamos algunos ejemplos de ecuaciones sin solución:

 

Ejemplo 1: un ejemplo de ecuación sin solución es la siguiente:

¿Hay ecuaciones sin solución? La respuesta es sí y proporcionamos ejemplos de ecuaciones que no tienen solución. Con ejemplos y ecuaciones resueltas. Secundaria. Álgebra. Matemáticas.

La ecuación no tiene solución porque si a x le sumamos 1, no puede ser igual a x. De hecho, si intentamos resolver la ecuación, obtenemos una igualdad FALSA:

¿Hay ecuaciones sin solución? La respuesta es sí y proporcionamos ejemplos de ecuaciones que no tienen solución. Con ejemplos y ecuaciones resueltas. Secundaria. Álgebra. Matemáticas.

 

Ejemplo 2:

¿Hay ecuaciones sin solución? La respuesta es sí y proporcionamos ejemplos de ecuaciones que no tienen solución. Con ejemplos y ecuaciones resueltas. Secundaria. Álgebra. Matemáticas.

Esta ecuación tampoco tiene solución porque una división nunca puede dar 0 como resultado (cociente).

 

Ejemplo 3:

¿Hay ecuaciones sin solución? La respuesta es sí y proporcionamos ejemplos de ecuaciones que no tienen solución. Con ejemplos y ecuaciones resueltas. Secundaria. Álgebra. Matemáticas.

Esta ecuación exponencial tampoco tiene solución porque ninguna potencia puede dar 0 como resultado:

¿Hay ecuaciones sin solución? La respuesta es sí y proporcionamos ejemplos de ecuaciones que no tienen solución. Con ejemplos y ecuaciones resueltas. Secundaria. Álgebra. Matemáticas.

 

Ejemplo 4:

¿Hay ecuaciones sin solución? La respuesta es sí y proporcionamos ejemplos de ecuaciones que no tienen solución. Con ejemplos y ecuaciones resueltas. Secundaria. Álgebra. Matemáticas.

El valor absoluto nunca puede ser negativo por su propia definición, por tanto, esta ecuación tampoco tiene solución.

Otros ejemplos de ecuaciones sin solución que se obtienen de la igualdad FALSA 1 = 2:

¿Hay ecuaciones sin solución? La respuesta es sí y proporcionamos ejemplos de ecuaciones que no tienen solución. Con ejemplos y ecuaciones resueltas. Secundaria. Álgebra. Matemáticas.

Más información y temas relacionados:

 

Posted on

¿Qué es una Ecuación?

Una ecuación es una igualdad entre dos expresiones algebraicas en las que aparece una (o más) incógnita. Normalmente, la incógnita es x. 

La incógnita x representa al número (o números), si existe, que hace que la igualdad sea verdadera. Este número desconocido es la solución de la ecuación.

Al cambiar la x por la solución, la igualdad debe ser cierta.

Ejemplo

x+2 = 2·x-1

  • Si x es 0, la igualdad no se cumple porque 0+2  no es igual a 2·0-1.
  • Si x es 3, la igualdad sí se cumple porque 3+2  es igual a 2·3-1.

La solución de la ecuación es x = 3.

Algunas cuestiones…

Algunas cuestiones que suelen hacerse los alumnos son las siguientes:

  • ¿Todas las ecuaciones tienen solución?
  • ¿Cuántas soluciones tiene una ecuación?
  • ¿Cuántos tipos de ecuaciones hay?
  • ¿Puede haber más de una incógnita?

Respuestas a las cuestiones:

En la siguiente página veremos algunos tipos de ecuaciones y cómo resolverlas:

Ecuaciones resueltas