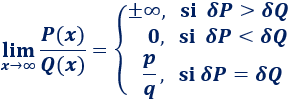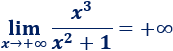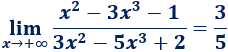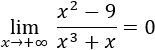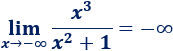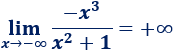En el límite de un cociente de polinomios P(x)/Q(x) suele aparecer un cociente de infinitos (∞/∞).
Escribimos δP y δQ para referirnos al grado de los polinomios P y Q, respectivamente. Entonces,
- En el primer caso, el signo del infinito depende de los grados de los polinomios y de sus coeficientes.
- En el tercer caso, p es el coeficiente director de P(x) y q es el de Q(x).
Ejemplo 1
El límite es infinito porque el grado del numerador es mayor que el del denominador. Los coeficientes de los polinomios son positivos y el infinito del límite es positivo, por tanto, el límite es positivo.
Ejemplo 2
Tenemos un cociente de polinomios de igual grado. Su límite es el cociente de sus coeficientes directores.
Ejemplo 3
El límite es 0 porque el grado del denominador es mayor.
Ejemplo 4
El límite es infinito porque el grado del numerador es mayor. Los coeficientes son positivos y el infinito del límite es negativo. Como el grado del numerador es impar y el del numerador es par, el resultado es negativo (negativo entre positivo).
Ejemplo 5
El límite es infinito porque el grado del numerador es mayor. El infinito del límite es negativo. Al cuadrado es positivo. Al cubo es negativo, pero tiene el coeficiente negativo. Por tanto, tenemos positivo entre positivo.
Ejemplo 6
El límite es infinito porque el grado del numerador es mayor. Positivo entre negativo, así que el resultado es negativo.
Más ejemplos y temas de límites:
- 50 límites resueltos
- Límites resueltos
- Límites laterales
- Indeterminación (límites de funciones)
- Indeterminación infinito menos infinito
- Indeterminación cero partido cero
- Indeterminación infinito partido infinito
- Indeterminación cero por infinito
- Indeterminación uno elevado a infinito
- Indeterminación cero elevado cero
- Indeterminación infinito elevado a cero
- Regla de L’Hôpital
- Infinitésimos equivalentes
- Teorema del emparedado
- Límites de sucesiones
- Definiciones formales de límites
- Criterio de la media geométrica y de la raíz
- Criterio de la media aritmética
- Criterio de Stolz del cociente