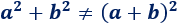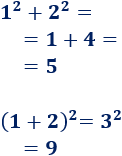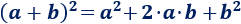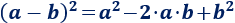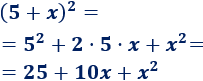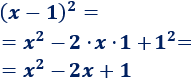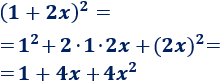Como regla general, el cuadrado de la suma es distinto de la suma de los cuadrados. Es decir,
Por ejemplo, si a = 1 y b = 2, la suma de sus cuadrados y el cuadrado de su suma son distintos:
Para calcular el cuadrado de una suma disponemos de una sencilla fórmula:
Lo mismo ocurre cuando se trata de una resta:
Veamos algunos ejemplos:
Ejemplo 1
Ejemplo 2
Ejemplo 3
Más ejemplos en