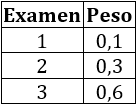
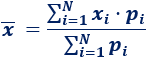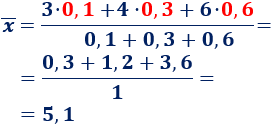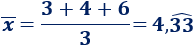En este post vamos a ver un importante teorema del cálculo diferencial: el teorema de Rolle.
Teorema de Rolle:
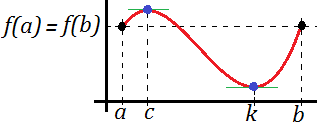
Sea f una función continua en el intervalo cerrado [a, b], derivable en el intervalo abierto ]a, b[ y con f(a) = f(b). Entonces, existe al menos un punto c del intervalo abierto ]a, b[ que anula a la derivada de f, es decir, f'(c)=0.
Interpretación:
Como la función es continua y f(a) = f(b), entonces hay dos opciones:
- La función es constante, es decir, f(x) = f(a) = f(b). En este caso, sabemos que la derivada de f se anula.
- La función no es constante y, por tanto, presenta algún máximo o mínimo. En estos puntos (los máximos o mínimos) es donde se anula la derivada.
Más información y temas relacionados:
- Michel Rolle y el teorema de Rolle
- Criterio de la primera derivada
- Criterio de la segunda derivada
- Condición necesaria de extremo relativo
- Máximos y mínimos de una función (1)
- Máximos y mínimos de una función (2)
- Problemas de optimizar
- Regla de l’Hôpital
- Funciones continuas (1)
- Funciones continuas (2)

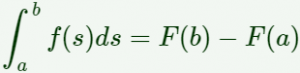
![la integral definida de f es el área de la región delimitada entre la gráfica de f, el eje OX en el intervalo [a,b] Issac Barrow (1630-1677): biografía, interpretación geométrica de la integral definida y demostración de la Regla de Barrow y del Teorema fundamental del cálculo](https://www.matesfacil.com/matematicos/Barrow/Barrow.png)