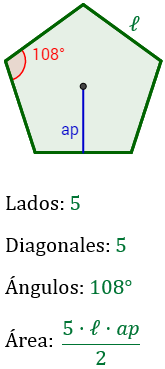
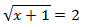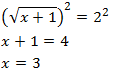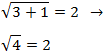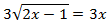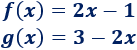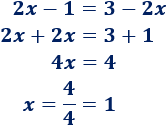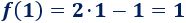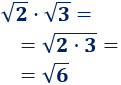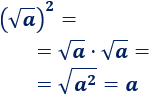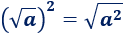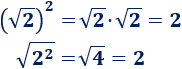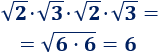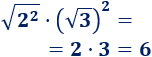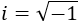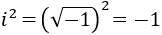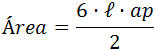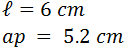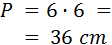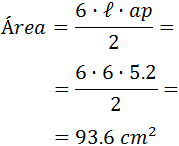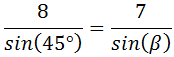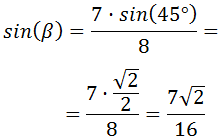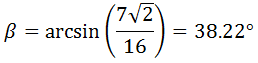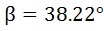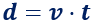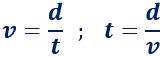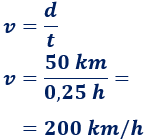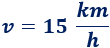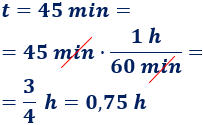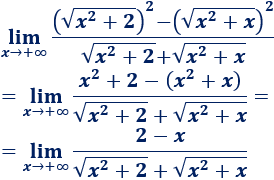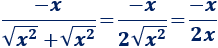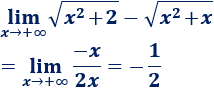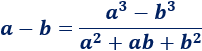Sin categoría – Page 4 – Matemáticas fáciles

19 agosto, 202014 septiembre, 2021

¿Qué es una ecuación irracional?

Una ecuación irracional es una ecuación en la que la incógnita se encuentra en una raíz.

Ejemplo de ecuación irracional sencilla:

Normalmente, para resolver este tipo de ecuaciones, elevamos al cuadrado ambos lados de la igualdad:

La raíz cuadrada desaparece al elevar al cuadrado porque son operaciones inversas.

Siempre que resolvemos una ecuación irracional tenemos que comprobar que la solución verifica la ecuación inicial.

Sustituimos x = 3 en la ecuación:

Por tanto, x = 3 es la solución.

Ejemplo 2

Elevamos al cuadrado ambos lados de la ecuación obteniendo una ecuación de segundo grado:

La única solución de la ecuación de segundo grado es x = 1. Comprobamos si es la solución de la ecuación irracional:

Por tanto, es la solución.

Más ejemplos y temas relacionados:

16 agosto, 20201 octubre, 2021

Interpretación geométrica de las ecuaciones

Comúnmente, se considera la solución de una ecuación como el valor que debe tomar x para que la igualdad de la ecuación se cumpla. Sin embargo, podemos ver una ecuación como una igualdad entre dos funciones. Para que sea más sencillo de explicar y entender, nos ayudaremos de un ejemplo.

Recordad que la gráfica de una función f es el conjunto de puntos (x, f(x)). Teniendo esto en cuenta, si la gráfica de la función f y de la función g se cortan, lo hacen en un punto común (a, b) siendo b = f(a) = g(a).

Ejemplo

Sea la ecuación de primer grado

Consideremos esta ecuación como una igualdad entre dos funciones:

Lógicamente, las funciones f y g son

Como f(x) es la imagen de x mediante f y g(x) es la imagen de x mediante g, al igualar f(x) = g(x), estamos igualando las imágenes de x mediante f y g. Por tanto, la solución de la ecuación f(x) = g(x) son los valores que debe tomar x para que f(x) = g(x) y son, por ende, las primeras coordenadas de los puntos de corte entre las gráficas de f y g.

Resolvemos la ecuación del ejemplo:

Como la ecuación sólo tiene una solución, las gráficas de f y de g se cortan en un único punto: el punto cuya primera coordenada es x = 1. Calculamos la segunda coordenada de dicho punto:

Luego el punto de corte de las gráficas de f y de g es (1, 1).

Gráficas:

Al considerar una ecuación como una igualdad entre funciones para hallar sus puntos de corte, es fácil ver que pueden darse las siguientes situaciones:

Una ecuación puede no tener solución (real). Ocurre cuando las dos gráficas no se cortan:

Una ecuación puede tener una única solución. Ocurre cuando las dos gráficas se cortan en un único punto:

Una ecuación puede tener varias soluciones. Ocurre cuando las dos gráficas se cortan en varios puntos:

Una ecuación puede tener infinitas soluciones. Ocurre cuando las dos gráficas son iguales (se cortan en todos sus puntos) o cuando se cortan en infinitos puntos pero no en todos:

Ahora bien, el número de soluciones dependerá de las funciones implicadas.

Más información y temas relacionados:

4 agosto, 202023 septiembre, 2021

Raíz cuadrada de una multiplicación

La raíz cuadrada de un producto de factores es igual al producto de las raíces cuadradas de los factores:

Por ejemplo, la raíz cuadrada de 2 por la de 3 es la raíz cuadrada de 6:

Como consecuencia,

La raíz cuadrada desaparece al elevar al cuadrado:

Además, de lo anterior se tiene que

Se puede introducir o extraer el cuadrado en una raíz cuadrada:

Por ejemplo,

Ejemplo 1 del uso de estas propiedades para calcular raíces:

Ejemplo 2

Más ejemplos y temas relacionados:

3 agosto, 202023 septiembre, 2021

¿Existe la raíz cuadrada de un número negativo?

Sí, existe la raíz cuadrada de un número negativo.

La unidad imaginaria se denota por i y se define como la raíz cuadrada de -1:

El cuadrado de la unidad imaginaria es -1:

Con la invención del número imaginario ya podemos trabajar con raíces cuadradas de números negativos (nos ayudaremos de la propiedad del producto de raíces).

Veamos algunos ejemplos:

Raíces cuadradas de -4:

Raíces cuadradas de -25:

Observad que, entonces, sí hay números cuyo cuadrado es negativo: los números imaginarios.

Por ejemplo,

Más ejemplos y temas relacionados:

14 julio, 202024 septiembre, 2021

Hexágono regular

El hexágono regular es el polígono regular de 6 lados.

Es decir, es el polígono que tiene 6 lados que miden lo mismo y sus ángulos internos miden 120º cada uno.

Lógicamente, el perímetro del hexágono regular de lado L es 6·L.

Para calcular el área necesitamos el lado, L, y el apotema, ap:

Ejemplo de aplicación: si el lado de un hexágono regular mide 6cm y su apotema mide 5.2cm,¿cuál es el perímetro y el área de dicho hexágono?

Los datos que tenemos son el lado y la apotema:

El perímetro es la suma de las longitudes de todos los lados. Como el hexágono es regular, todos sus 6 lados miden lo mismo, así que su perímetro es

La fórmula del área del hexágono regular es

Como tenemos el lado y la apotema, sólo tenemos que sustituirlos en la fórmula:

Nota: no olvidemos que las unidades del área son al cuadrado.

Más ejemplos y temas relacionados:

9 julio, 202024 septiembre, 2021

Pentágono regular

Un pentágono regular es un polígono regular de 5 lados.

Los 5 lados del pentágono regular miden lo mismo y sus ángulos interiores miden 108º.

Como tiene 5 lados iguales, el perímetro de un pentágono regular de lado L es P = 5·L.

Para calcular el área del pentágono regular se necesita su lado, L, y su apotema, ap:

Ejemplo de aplicación: Si el área de un pentágono regular es 5m² y su apotema mide 1.17m, ¿Cuánto miden sus lados?

Como el pentágono es regular, su área viene dada por la fórmula

Como sabemos que el área es 5m² y que la apotema mide 1.17m, al sustituir en la fórmula anterior, tenemos

De la expresión anterior podemos despejar L, que es la longitud de los lados del pentágono:

Como el área es en metros cuadrados, la medida obtenida es en metros.

Luego los lados del pentágono miden 1.71m.

Más ejemplos y temas relacionados:

30 junio, 202014 septiembre, 2021

Sólidos platónicos

Los sólidos platónicos son las siguientes figuras:

El tetraedro tiene 4 caras.
El hexaedro tiene 6 caras.
El octaedro tiene 8 caras.
El dodecaedro tiene 12 caras.
El icosaedro tiene 20 caras.

Los sólidos platónicos tienen propiedades comunes, por ejemplo:

Todas las caras son polígonos regulares iguales.
Todos los ángulos (diedros) son iguales.
Todas las aristas tienen la misma longitud.
En todos los vértices concurren el mismo número de caras y de aristas.

Y, seguramente, la propiedad más importante es:

Sólo existen cinco poliedros regulares y son los expuestos anteriormente.

Más información y temas de geometría:

23 junio, 202021 septiembre, 2021

Teorema del seno

El teorema del seno es un conocido e importante resultado de trigonometría que dice así:

Sea un triángulo cualquiera con lados a, b y c y con ángulos interiores α, β y γ (son los ángulos opuestos a los lados, respectivamente). Entonces, se cumple la relación

Veamos dos ejemplos de aplicación:

Ejemplo 1: en el siguiente triángulo de lados a = 8cm y b = 7cm. Calcular cuánto mide el ángulo β sabiendo que el ángulo γ mide 45º.

Como conocemos los lados a y b y el ángulo α, aplicamos el teorema del seno:

Por tanto,

Despejamos el seno de β:

Finalmente, despejamos β utilizando la inversa del seno (arcoseno):

Luego el ángulo es

Ejemplo 2: se tiene un triángulo con ángulos α = 67° y β = 36° y un lado a = 6cm. ¿Cuánto mide el lado c?

Para calcular el lado c necesitamos conocer el ángulo γ.

Recordemos que en todo triángulo la suma de sus ángulos internos es 180°, es decir, tenemos la ecuación:

Despejamos el ángulo γ:

Sustituimos los valores:

Luego el ángulo es γ = 77º.

Ahora podemos aplicar el teorema del seno:

Sustituimos los datos:

Por tanto,

Luego el lado c mide 6.35 cm.

Más ejemplos y temas relacionados:

12 junio, 202012 septiembre, 2021

Fórmula del movimiento rectilíneo uniforme (MRU)

Un móvil realiza un movimiento rectilíneo uniforme cuando:

Se mueve en línea recta (rectilíneo)
Su velocidad es constante (uniforme)

En este movimiento, la fórmula más sencilla es la siguiente:

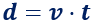
siendo

d la distancia recorrida,
v la velocidad del móvil
t el tiempo que dura el movimiento

Para calcular la velocidad o el tiempo, despejamos en la ecuación anterior:

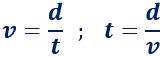
Esta fórmula nos indica que

La distancia recorrida es directamente proporcional a la velocidad y al tiempo.
La velocidad y el tiempo son inversamente proporcionales entre sí.

Esto significa:

Cuanto mayor es la velocidad o el tiempo, mayor es la distancia recorrida.
Cuanto mayor es la velocidad, menos tiempo se requiere para recorrer una distancia.

Ejemplo 1:

Si un móvil que se mueve a velocidad constante recorre 1km en 10 minutos, entonces en 20 minutos recorre 2km.

Generalmente, expresamos

la velocidad en km/h (kilómetros por hora)
el tiempo en h (horas)
la distancia recorrida en km (kilómetros)

Para poder aplicar la fórmula, debemos asegurarnos de que las unidades de medida sean acordes. No podemos escribir la velocidad en km/h y el tiempo en min (minutos) o la distancia recorrida en m (metros).

Ejemplo 2: ¿A qué velocidad debe circular un auto de carreras para recorrer 50km en un cuarto de hora?

Como la distancia es en kilómetros, vamos a escribir el tiempo en unidades de hora para tener la velocidad en km/h.

El tiempo que dura el movimiento es

La distancia recorrida por el móvil es

Por tanto, su velocidad debe ser

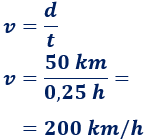
Ejemplo 3: Una bicicleta circula en línea recta a una velocidad de 15km/h durante 45 minutos. ¿Qué distancia recorre?

La velocidad de la bicicleta es

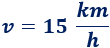
El tiempo que dura el movimiento es

Como las unidades de velocidad son kilómetros por hora y el tiempo está en minutos, tenemos que pasar el tiempo t de minutos a horas (dividiendo entre 60):

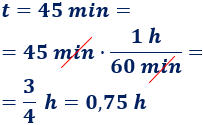
Calculamos la distancia que recorre la bicicleta:

Más ejemplos y temas relacionados:

14 mayo, 2020

Límites de restas de raíces

Anteriormente, vimos cómo calcular el límite de una raíz y el límite de una fracción de raíces. En este post explicamos cómo calcular límites de restas de raíces.

Para calcular el límite de una resta de raíces cuadradas usaremos la fórmula