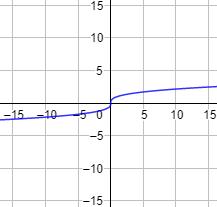
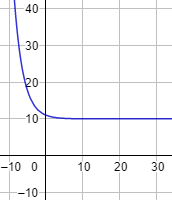
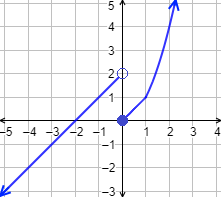
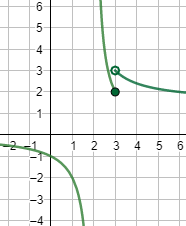
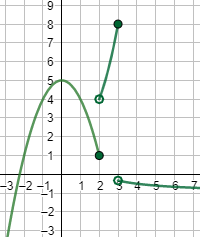
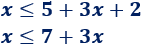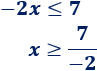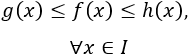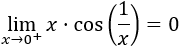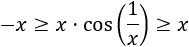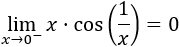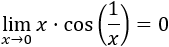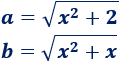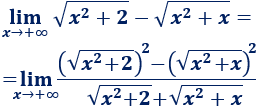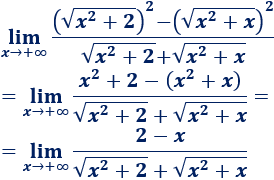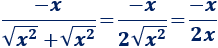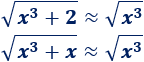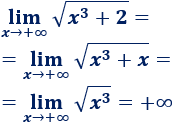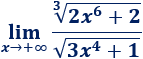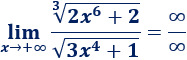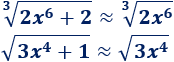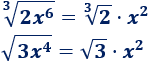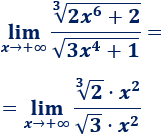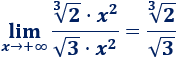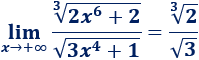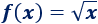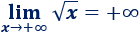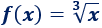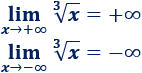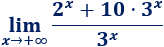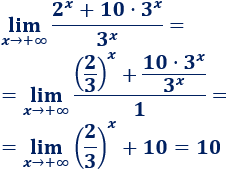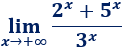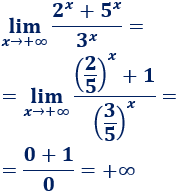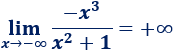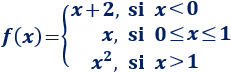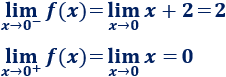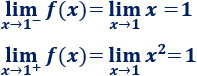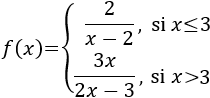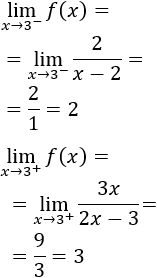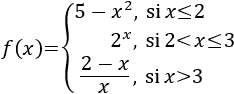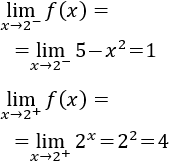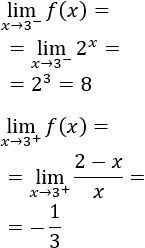¿Qué es una inecuación?

Una inecuación es una desigualdad entre dos expresiones algebraicas con una o varias incógnitas.

Los signos de desigualdad posibles son cuatro: <, ≤, > y ≥. Significado:

a < b significa que a es menor que b. Por ejemplo, 2 < 3.
a ≤ b significa que a es menor o igual que b. Por ejemplo, 2 ≤ 3.
a > b significa que a es mayor que b. Por ejemplo, 3 > 2.
a ≥ b significa que a es mayor o igual que b. Por ejemplo, 2 ≥ 2.

En este post veremos sólo inecuaciones con una sólo incógnita: x.

Ejemplo 1 :

La solución o soluciones de esta inecuación son los números que al restarle 2 son mayor que 1. Esto ocurre con cualquier número mayor o igual que 3. Por tanto, las soluciones de la inecuación son los número x tales que x > 3.

Otra forma de expresar la solución es en forma de intervalo:

$Explicamos qué son las inecuaciones y cómo resolverlas, desde inecuaciones sencillas a otras más difíciles. Ecuaciones simples, con fracciones y con polinomios de segundo grado. Álgebra. Matemáticas. Inecuaciones resueltas.$

Representación en la recta real:

Al igual que en las ecuaciones, los sumandos de las inecuaciones pueden pasar al otro lado cambiando su signo.

Ejemplo 2 :

Como la x está restando, puede pasar al otro lado sumando:

El 2 pasa al otro lado restando:

La solución de la inecuación es x ≤ 1, o bien,

Representación:

Los coeficientes de la x también pueden pasar al otro lado como en las ecuaciones, pero tenemos que cambiar el signo de desigualdad si el número es negativo.

Ejemplo 3:

Pasamos el 2 al otro lado:

Pasamos el 3x de la derecha al otro lado:

El coeficiente de la x es -2. Puede pasar al otro lado dividiendo, pero tenemos que cambiar el signo de desigualdad porque el -2 es negativo (de menor o igual a mayor o igual):

La solución de la inecuación es x ≥ -7/2.

Representación:

Más ejemplos y temas relacionados:

27 mayo, 202013 septiembre, 2021

Gráfica de una función

La gráfica de una función matemática es su representación gráfica, la cual nos permite observar el comportamiento o propiedades de la misma. También, podemos obtener la imagen de un número a partir de la gráfica.

Recordamos que si y = f(x) es una función, entonces la imagen de un número a es b = f(a). Por ejemplo, consideremos la función f(x) = 2x + 1. Para calcular la imagen de un número, tenemos que sustituir x por dicho número:

Es decir,

La imagen de 0 es 1.
La imagen de 1 es 3.
La imagen de 2 es 5.

Si a es un número y b es su imagen, es decir, b = f(a), entonces el punto (a, b) es un punto de la gráfica de f. Como hemos calculado varias imágenes, tenemos varios puntos:

f(0) = 1 → tenemos el punto (0, 1).
f(1) = 3 → tenemos el punto (1, 3).
f(2) = 5 → tenemos el punto (2, 5).

Si representamos estos puntos en el plano y los unimos, tenemos la gráfica de la función:

La gráfica de esta función es una recta.

Observando la gráfica, podemos deducir, por ejemplo, que la imagen de 3 es 7, es decir, f(3) = 7, ya que el punto (3, 7) está en la gráfica de f.

Como decíamos anteriormente, la gráfica permite observar el comportamiento de la función. Por ejemplo:

La gráfica de esta función es una recta, pero las gráficas de las funciones también pueden ser curvas, por ejemplo.
La recta es creciente (vista de izquierda a derecha), lo que significa que si a < b, entonces f(a) < f(b).
Los puntos de corte con los ejes. Por ejemplo, la gráfica corta al eje Y en el punto (0, 1).
Es una función continua, lo que significa que puede dibujarse de un solo trazo, lo cual no siempre es así.

Otros ejemplos de gráficas

La gráfica de la función f(x) = x² es una parábola (una curva):

La gráfica de la función f(x) = 1/x NO es continua (tiene un salto):

La gráfica de la función f(x) = x³ -3x es creciente, decreciente y creciente (de izquierda a derecha):

La gráfica de la función f(x) = cos(x) es periódica (se repite):

Más información en

Otros temas relacionados:

21 mayo, 202011 septiembre, 2021

Teorema del sándwich o del emparedado

El teorema del sándwich establece que si una función f(x) se encuentra entre dos funciones g(x) y h(x), es decir,

Y los límites de g(x) y de h(x) existen y son iguales, entonces el límite de f(x) también existe y coincide con el de g(x) y el de h(x).

Veamos un par de ejemplos de la importancia del teorema del sándwich en la práctica demostrando límites.

Ejemplo 1

En principio, este límite no es sencillo de calcular, puesto que la función seno es una función periódica que toma valores en el intervalo [-1, 1], por lo que el límite cuando x tiende a infinito es indeterminado.

Así, pues, vamos a acotar la función sin(x)/x entre dos funciones con límite.

Como el seno toma valores entre -1 y 1, podemos escribir

Dividimos entre x:

Ya tenemos la función acotada entre dos funciones (siempre que x sea mayor que 0) y estas funciones tienen límite cuando x tiende a infinito y es 0.

Por tanto, la función sin(x)/x también tiene límite y es 0:

Ejemplo 2

El coseno es una función periódica con valores en el intervalo [-1, 1], aunque existe su límite cuando x tiende a 0 y es cos(0) = 1. Sin embargo, en la función del límite el argumento del coseno es 1/x, el cual tiende a infinito cuando x tiende a 0. Además, el coseno del límite está además multiplicado por x.

A pesar de todo esto, el límite es sencillo de calcular mediante el teorema del sándwich. Acotamos el coseno:

Supongamos que x>0, entonces

Por el teorema del emparedado,

Ahora, hacemos lo mismo suponiendo que x<0:

Por el teorema del emparedado,

Como los límites laterales coinciden,

Gráfica de la función:

Más ejemplos en Teorema del emparedado o del sándwich.

Otros temas relacionados:

14 mayo, 2020

Límites de restas de raíces

Anteriormente, vimos cómo calcular el límite de una raíz y el límite de una fracción de raíces. En este post explicamos cómo calcular límites de restas de raíces.

Para calcular el límite de una resta de raíces cuadradas usaremos la fórmula

Ejemplo 1

En un principio, tenemos la indeterminación infinito menos infinito. Sin embargo, podemos aplicar la fórmula anterior para evitarla.

Llamamos

Aplicando la fórmula,

Las raíces del numerador desaparecen por estar elevadas al cuadrado:

Como los monomios de mayor grado son los importantes para calcular el límite de una raíz, cuando x es grande, la función del límite es similar a

Por tanto,

Para calcular el límite de una resta de raíces cúbicas usaremos la fórmula

Más información y ejemplos:

14 mayo, 202014 mayo, 2020

Límites de fracciones de raíces

Anteriormente, vimos cómo calcular el límite de una raíz. En este post explicamos cómo calcular límites de fracciones de raíces.

La técnica que usaremos es omitir los sumandos irrelevantes de los radicandos.

Supongamos que tenemos las siguientes funciones que son raíces cuadradas de polinomios de tercer grado:

Los límites dependen de los monomios de grado mayor (en nuestro caso, es el monomio x³). Esto de sebe a que estos monomios son los que más peso tienen en la suma cuando x toma valores muy grandes (o muy pequeños).

Como las tres funciones tienen un polinomio del mismo grado (grado 3), su comportamiento es similar cuando x toma valores grandes, como se observa en sus gráficas:

Podríamos decir que las funciones son casi iguales:

Esto nos facilita el cálculo de límites: los tres límites de estas funciones coinciden:

Importante: no hay que aplicar este procedimiento cuando tenemos una resta de raíces.

A continuación, explicamos cómo aplicar la técnica anterior para calcular límites de cocientes de raíces.

Supongamos que tenemos un cociente de raíces de distinto orden:

Cuando x tiende a +∞, los radicandos tienden a infinito y, por tanto, tenemos un cociente de infinitos:

Sin embargo, podemos cambiar las raíces por raíces casi iguales, según vimos anteriormente:

Además, podemos aplicar las propiedades de las raíces/potencias:

Por tanto, podemos ver el límite inicial como un cociente de polinomios:

Recordad que el límite del cociente de dos polinomios del mismo grado es igual al cociente de sus coeficientes principales:

Por tanto,

Más información y ejemplos:

14 mayo, 202014 mayo, 2020

Límite de una raíz

En este post explicamos cómo calcular límites de raíces. Próximamente, veremos cómo calcular límites de divisiones de raíces y límites de restas de raíces.

Consideremos la función raíz cuadrada:

Se trata de una función que siempre crece, así que su límite es infinito cuando x tiende a infinito positivo:

La función no está definida cuando x es negativo (no existe la raíz cuadrada de un número negativo), así que no existe el límite cuando x→-∞.

Gráfica:

Consideremos ahora la función raíz cúbica:

La raíz cúbica de x crece cuando x crece y decrece cuando x decrece, así que sus límites son

Gráfica:

Más información y ejemplos:

9 abril, 2020

Límite de una fracción con exponenciales

Vimos en límites de exponenciales cómo calcular límites de funciones exponenciales según el valor de la base. En este post explicamos cómo calcular límites de cocientes/fracciones con exponenciales.

La técnica es muy sencilla:

Dividimos en el numerador y en el denominador por la exponencial de base mayor.

Ejemplo 1

La exponencial de base mayor es 3^x, así que dividimos entre 3^x:

Observad que la exponencial de base 2/3 tiende a 0 porque 2/3 es menor que 1.

Gráfica de la función:

Ejemplo 2

La exponencial de base mayor es 5^x, así que dividimos entre 5^x:

Gráfica de la función:

Ejemplo 3

La exponencial de base mayor es 3^x, así que dividimos entre 3^x:

Gráfica de la función:

Más información y ejemplos:

8 abril, 20208 abril, 2020

Límites de exponenciales

El límite de una exponencial depende, sobre todo, de la base de la exponencial.

Límite cuando x→+∞

Supongamos que x tiende a +∞ , entonces

Si la base es mayor que 1, el límite es infinito positivo. Por ejemplo,

Si la base está entre 0 y 1, el límite es 0. Por ejemplo,

Si la base es 1, el límite es 1:

Importante: si se trata de una función exponencial cuya base tiende a 1 y cuyo exponente tiende a infinito, entonces tenemos la indeterminación 1 elevado a infinito.

Límite cuando x→-∞

Supongamos que x tiende a -∞ , entonces

Si la base es mayor que 1, el límite es 0. Por ejemplo,

Si la base está entre 0 y 1, el límite es infinito. Por ejemplo,

Si la base es 1, el límite es 1 (también hay que tener en cuenta lo dicho en el tercer caso anterior).

Más información y ejemplos en

21 febrero, 2020

Límite de una fracción de polinomios

En el límite de un cociente de polinomios P(x)/Q(x) suele aparecer un cociente de infinitos (∞/∞).

Escribimos δP y δQ para referirnos al grado de los polinomios P y Q, respectivamente. Entonces,

En el primer caso, el signo del infinito depende de los grados de los polinomios y de sus coeficientes.
En el tercer caso, p es el coeficiente director de P(x) y q es el de Q(x).

Ejemplo 1

El límite es infinito porque el grado del numerador es mayor que el del denominador. Los coeficientes de los polinomios son positivos y el infinito del límite es positivo, por tanto, el límite es positivo.

Ejemplo 2

Tenemos un cociente de polinomios de igual grado. Su límite es el cociente de sus coeficientes directores.

Ejemplo 3

El límite es 0 porque el grado del denominador es mayor.

Ejemplo 4

El límite es infinito porque el grado del numerador es mayor. Los coeficientes son positivos y el infinito del límite es negativo. Como el grado del numerador es impar y el del numerador es par, el resultado es negativo (negativo entre positivo).

Ejemplo 5

El límite es infinito porque el grado del numerador es mayor. El infinito del límite es negativo. Al cuadrado es positivo. Al cubo es negativo, pero tiene el coeficiente negativo. Por tanto, tenemos positivo entre positivo.

Ejemplo 6

El límite es infinito porque el grado del numerador es mayor. Positivo entre negativo, así que el resultado es negativo.

Más ejemplos y temas de límites:

20 febrero, 202011 septiembre, 2021

Ejemplos de continuidad de funciones definidas a trozos

La continuidad de una función definida a trozos o por intervalos se estudia del mismo que una función normal, pero hay que tratar los puntos donde cambia la definición de la función como posibles puntos de discontinuidad. En estos puntos, tenemos que comprobar si los límites laterales coinciden.

Veamos algunos ejemplos.

Ejemplo 1

La función es continua en cada uno de los tres intervalos puesto que se tratan de polinomios. Los posibles candidatos a puntos de discontinuidad son los extremos de los intervalos: x=0 y x=1.

Calculamos los límites laterales en estos puntos:

Punto x=0

Punto x=1

El único punto de discontinuidad es x=0, ya que los límites laterales no coinciden.

Gráfica:

Ejemplo 2

En el intervalo x≤3, la función es racional. Tenemos que excluir el punto x=2 del dominio porque anula al denominador.
En el intervalo x>3, también es racional. El denominador se anula en x=3/2 <3, así que no hay que excluir ningún punto.

El dominio de la función es el conjunto de los reales excepto x=2.

Calculamos los límites laterales en el punto x=3: